Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Chute d'un parachutiste - Exercice 1

30 min
45
Un exemple d'une équation différentielle linéaire du premier ordre en Mécanique classique du point.
Question 1
Vous arrondirez l'ensemble de vos résultats numérique au dixième.
Dans le référentiel terrestre, supposé galiléen le temps de l'expérience considérée, la trajectoire du centre de gravité GG d'un homme chutant suspendant à un parachute suit une verticale terrestre.

Pour paramétrer ce mouvement, on utilisera un axe descendant d'origine OO prise à la sortie de l'avion. On notera par k⃗\vec{k} le vecteur unitaire ∣∣ k⃗ ∣∣=1\vert \vert \, \vec{k} \, \vert \vert =1 orienté vers le bas de cet axe.
A un instant tt donné, la vitesse du centre de gravité GG est noté v⃗G(t)=vG(t) k⃗\vec{v}_G(t) = v_G(t) \, \vec{k}. Dans cette relation, vGv_G est une fonction numérique de la variable temporelle tt.
L'ensemble à une masse m=80 kgm = 80 \, kg, et évolue dans le champs de pesanteur terrestre g⃗\vec{g} telle que g=∣∣ g⃗ ∣∣=9,8 m.s−2g = \vert \vert \, \vec{g} \, \vert \vert = 9,8 \, m.s^{-2}.
On admettra que le parachutiste est, dans sa globalité, soumis à deux forces :
  ∙  \,\, \bullet \,\, Son propres poids P⃗=mg⃗\vec{P} = m \vec{g} ;
  ∙  \,\, \bullet \,\, Les forces de frottement de l'air f⃗=−rv⃗G\vec{f} = - r \vec{v}_G où rr est un coefficient de frottement de valeur r=112  U.S.I.r = 112 \,\, U.S.I. (UUnité du SSystème IInternational).
En appliquant la deuxième loi de Newton (encore appelée Relation Fondamentale de la Dynamique) au centre de gravité GG, on admet que l'on obtient l'équation différentielle, notée (E)(E), suivante :
m vG′(t)+r vG(t)=mg m \, v'_G(t) + r \,v_G(t) = mg
Il s'agit d'une équation différentielle linéaire, à coefficients constants et avec second membre mgmg constant (uniforme et stationnaire dans le langage du physicien).
L'instant initial est celui de l'ouverture du parachute.

Déterminer la solution homogène vG/H(t)v_{G/H}(t) associée à cette équation différentielle (E)(E), mais sans son second membre.

Correction
La solution homogène vG/H(t)v_{G/H}(t) associée à cette équation différentielle sans second membre est :
vG/H(t)=Ke−rmt      (K∈R)v_{G/H}(t) = K e^{-\frac{r}{m}t} \,\,\,\,\,\, (K \in \mathbb{R})
Question 2

Démontrer qu'une fonction constante réelle CC est une solution particulière de l'équation différentielle (E)(E), et en déterminer son expression en fonction de mm, gg et rr.

Correction
On a :
m C′+r C=mg     ⟺     m×0+r C=mg     ⟺     r C=mgm \,C' + r \,C = mg \,\,\,\,\, \Longleftrightarrow \,\,\,\,\, m \times 0 + r \,C = mg \,\,\,\,\, \Longleftrightarrow \,\,\,\,\, r\,C=mg
Soit :
C=mgrC=\dfrac{mg}{r}
Finalement :
vG/P(t)=mgrv_{G/P}(t)=\dfrac{mg}{r}
Question 3

En déduire la solution globale vG(t)v_G(t) de l'équation différentielle (E)(E).

Correction
La solution globale vG(t)v_G(t) de l'équation différentielle (E)(E) est la somme des deux précédentes, à savoir :
vG(t)=vG/H(t)+vG/P(t)v_{G}(t) = v_{G/H}(t) + v_{G/P}(t)
D'où
vG(t)=Ke−rmt+mgr      (K∈R)v_{G}(t) = K e^{-\frac{r}{m}t} + \dfrac{mg}{r} \,\,\,\,\,\, (K \in \mathbb{R})
Question 4

Si, initialement, on a la condition vG(t=0)=v0v_G(t=0) = v_0, déterminer l'expression littérale de la solution de ce problème.

Correction
On a :
vG(t=0)=Ke−rm×0+mgr     ⟺     v0=K+mgrv_{G}(t=0) = K e^{-\frac{r}{m}\times 0} + \dfrac{mg}{r} \,\,\,\,\, \Longleftrightarrow \,\,\,\,\, v_0 = K + \dfrac{mg}{r}
D'où l'égalité :
K=v0−mgrK = v_0 - \dfrac{mg}{r}
Ce qui implique que :
vG(t)=(v0−mgr)e−rmt+mgrv_{G}(t) = \left(v_0 - \dfrac{mg}{r} \right) e^{-\frac{r}{m}t} + \dfrac{mg}{r}
En factorisant par mgr\dfrac{mg}{r}, on trouve que :
vG(t)=mgr(1−e−rmt)+v0e−rmtv_{G}(t) = \dfrac{mg}{r} \left( 1 - e^{-\frac{r}{m}t} \right) + v_0 e^{-\frac{r}{m}t}
Question 5

Démontrer qu'il existe une vitesse limite vℓv_\ell atteinte par le parachutiste lorsque t⟶+∞t \longrightarrow +\infty. Faire l'application numérique.

Correction
On a :
vℓ=lim⁡t⟶+∞vG(t)=lim⁡t⟶+∞(mgr(1−e−rmt)+v0e−rmt)=mgrlim⁡t⟶+∞(1−e−rmt)+v0lim⁡t⟶+∞e−rmtv_\ell = \lim_{t \longrightarrow +\infty} v_{G}(t) = \lim_{t \longrightarrow +\infty} \left( \dfrac{mg}{r} \left( 1 - e^{-\frac{r}{m}t} \right) + v_0 e^{-\frac{r}{m}t} \right) = \dfrac{mg}{r} \lim_{t \longrightarrow +\infty} \left( 1 - e^{-\frac{r}{m}t} \right) + v_0 \lim_{t \longrightarrow +\infty} e^{-\frac{r}{m}t}
Soit :
vℓ=mgr(lim⁡t⟶+∞1−lim⁡t⟶+∞e−rmt)+v0lim⁡t⟶+∞e−rmt=mgr(1−0)+v0×0v_\ell = \dfrac{mg}{r} \left( \lim_{t \longrightarrow +\infty} 1 - \lim_{t \longrightarrow +\infty} e^{-\frac{r}{m}t} \right) + v_0 \lim_{t \longrightarrow +\infty} e^{-\frac{r}{m}t}= \dfrac{mg}{r} \left(1 - 0 \right) + v_0 \times 0
Finalement, on obtient :
vℓ=mgrv_\ell = \dfrac{mg}{r}
L'application numérique nous donne :
vℓ=80×9,8112     ⟺     vℓ=7  m.s−1v_\ell = \dfrac{80 \times 9,8}{112} \,\,\,\,\, \Longleftrightarrow \,\,\,\,\, v_\ell = 7 \,\, m.s^{-1}
Question 6

Tracer soigneusement la courbe représentative de la solution vG(t)v_G(t) ainsi trouvée, en prenant v0=16  m.s−1v_0 = 16 \,\, m.s^{-1} comme vitesse à l'instant de l'ouverture du parachute.

Correction
On a la solution suivante :
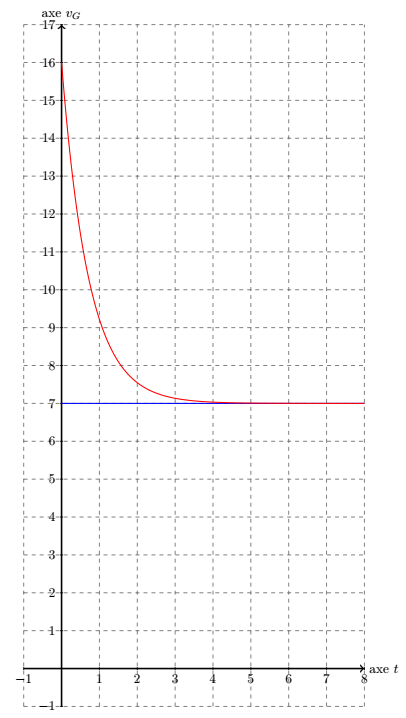vG(t)=vℓ(1−e−rmt)+v0e−rmtv_{G}(t) = v_\ell \left( 1 - e^{-\frac{r}{m}t} \right) + v_0 e^{-\frac{r}{m}t}
On peut considérer qu'au bout d'une durée de 44 secondes, après ouverture du parachute, le parachutiste à atteint sa vitesse limite vℓv_\ell (donc maximale).