Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Sujet 2 : avec de la Physique - Exercice 1
1 h 30 min
125
Les lois de la Physique nécessitent l’usage des outils, concepts, propriétés et objets mathématiques pour s'exprimer. L'intégration intervient dans de très nombreux domaines physiques et de l'ingénierie. Citons, par exemple, l'Electromagnétisme, la Mécanique, la Thermodynamique, la Relativité, la théorie du Signal, la Mécanique des Fluides, l'Electronique … etc. Nous allons illustrer cela dans le cadre de la Spectroscopie. Cette dernière est l'étude, et la description, des émissions et absorptions de lumières d'un gaz d'atomes ou de molécules. Historiquement, la Spectroscopie est une des raisons de la naissance et création de la Mécanique Quantique.
Le physicien est souvent confronté à des calculs techniques et parfois longs. C'est pourquoi une bonne compréhension des lois Physiques nécessite une bonne maîtrise de l'arsenal Mathématiques.
Le physicien est souvent confronté à des calculs techniques et parfois longs. C'est pourquoi une bonne compréhension des lois Physiques nécessite une bonne maîtrise de l'arsenal Mathématiques.
Question 1
Ce problème a pour but de calculer l'intégrale suivante :
Le terme s'appelle l'excenticité, et vérifie : .
Le terme s'appelle l'excenticité, et vérifie : .
A l'aide d'une intégration par parties, montrer que l'on peut mettre l'intégrale cherchée sous la forme suivante :
Correction
On utilise une intégration par parties. En effet, on a :
On remarque alors que le terme est assez proche de la dérivée, par rapport à la variable , de . En effet :
Ainsi, on en déduit que :
Donc, une intégration par parties nous conduit à :
Soit :
Comme , on en déduit que le terme entre crochet est nul. On a alors :
On remarque alors que le terme est assez proche de la dérivée, par rapport à la variable , de . En effet :
Ainsi, on en déduit que :
Donc, une intégration par parties nous conduit à :
Soit :
Comme , on en déduit que le terme entre crochet est nul. On a alors :
Question 2
Démontrer que l'on a la relation suivante : .
Correction
On sait que :
Soit :
Ainsi :
Donc, on en déduit que :
Soit :
Ce qui nous permet d'écrire que :
Soit encore :
Ce qui nous conduit bien à la relation proposée, à savoir :
Soit :
Ainsi :
Donc, on en déduit que :
Soit :
Ce qui nous permet d'écrire que :
Soit encore :
Ce qui nous conduit bien à la relation proposée, à savoir :
Question 3
Afin de calculer l'intégrale on pose le changement de variable . Dans ce cas, montrer que .
Correction
On a :
En utilisant la dérivée composée, on trouve que :
Soit :
Ainsi, on en déduit que :
Et donc :
Finalement, on trouve bien que :
En utilisant la dérivée composée, on trouve que :
Soit :
Ainsi, on en déduit que :
Et donc :
Finalement, on trouve bien que :
Question 4
En posant le changement de variable , montrer que .
Correction
On a :
Mais, on sait que pour , on a . Ainsi, on obtient :
On a :
Soit :
De plus, pour toute quantité réelle , on a : . Donc, on en déduit que :
Fianelement, on trouve que :
Mais, on sait que pour , on a . Ainsi, on obtient :
On a :
Soit :
De plus, pour toute quantité réelle , on a : . Donc, on en déduit que :
Fianelement, on trouve que :
Question 5
Comme la fonction tangente n'est pas définie en , alors le terme n'est pas défini en . C'est pourquoi on pose : . Dans ce cas, montrer que l'on a : .
Correction
Comme , on en déduit que si alors . Puis, si alors .
On a alors le changement d'écriture suivant :
Soit :
Soit encore :
Ce qui nous donne :
On a donc bien :
On a alors le changement d'écriture suivant :
Soit :
Soit encore :
Ce qui nous donne :
On a donc bien :
Question 6
Si une fonction est continue, strictement monotone et dérivable sur un intervalle de , et si sa dérivée ne s'annule pas sur , alors sa fonction réciproque est dérivable sur f(I). Et on a . Ceci s'écrit encore : .
Dans ce cas, par application de la formule de dérivation composée, on a :
Ce qui implique que :
Posons , on sait que la fonction tangente est strictement croissante et dérivable sur l'intervalle de , et que sa fonction dérivée est telle que . Dans ce cas on note par .
Démontrer que, pour tout réel, on a :
Le graphe représentatif de la fonction est le suivant :
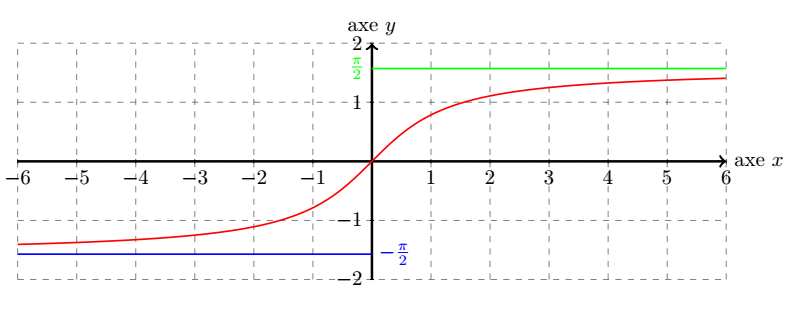
On constate alors que :
Dans ce cas, par application de la formule de dérivation composée, on a :
Ce qui implique que :
Posons , on sait que la fonction tangente est strictement croissante et dérivable sur l'intervalle de , et que sa fonction dérivée est telle que . Dans ce cas on note par .
Démontrer que, pour tout réel, on a :
Le graphe représentatif de la fonction est le suivant :

On constate alors que :
Correction
Soit un réel. On a :
Or, comme les fonction et sont réciproque l'une de l'autre, alors . Dans ce cas, on obtient :
Or, comme les fonction et sont réciproque l'une de l'autre, alors . Dans ce cas, on obtient :
Question 7
Soit un réel, et soit un réel strictement positif. Déterminer la dérivée, par rapport à , de l'expression .
Correction
On a :
Soit :
Finalement :
Soit :
Finalement :
Question 8
Démontrer que l'intégrale : .
Correction
On a :
On constate que alors il est possible de poser . On en déduit alors que . Dans ce cas . On a alors :
D'après la question précédente, on obtient :
Soit :
Ce qui nous donne encore :
Soit encore :
Ainsi, on peut écrire que :
Ce qui nous permet d'écrire que :
D'après le graphe de la fonction , on sait que . Donc :
Lorsque le terme et dans ce cas le terme , ceci car . D'après le graphe de la fonction , on sait que . Donc, on en déduit que :
Dans ce cas, on trouve que :
Finalement, on a bien :
On constate que alors il est possible de poser . On en déduit alors que . Dans ce cas . On a alors :
D'après la question précédente, on obtient :
Soit :
Ce qui nous donne encore :
Soit encore :
Ainsi, on peut écrire que :
Ce qui nous permet d'écrire que :
D'après le graphe de la fonction , on sait que . Donc :
Lorsque le terme et dans ce cas le terme , ceci car . D'après le graphe de la fonction , on sait que . Donc, on en déduit que :
Dans ce cas, on trouve que :
Finalement, on a bien :
Question 9
En déduire la valeur de l'intégrale recherchée initialement.
Correction
D'après la question 2, on sait que :
Ce qui nous donne
Soit :
Finalement, on obtient le résultat suivant :
Ce qui nous donne
Soit :
Finalement, on obtient le résultat suivant :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.