Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Sujet 1 - Exercice 1
1 h
90
Voici un problème. C'est donc plus long et plus technique et transversal.
Question 1
Soit et deux nombres réels strictement positifs.
On considère la fonction définie sur par :
On considère la fonction définie sur par :
Etudier les variations de . Montrer que la dérivée seconde s'annule une, et une seule, fois sur l'intervale .
Correction
La fonction est définie sur par :
On constate alors qu'elle est de classe sur et qu'elle est paire.
La présence du terme nous invite à vérifier sa périodicité. La présence du carré sur le cosinus nous laisse penser qu'elle peut-être de période . Vérifions ceci. Soit un réel. On a alors :
Ainsi, effectivement, est périodique. La conséquence de cette périodicité est qu'il est possible d'étudier les variations de sur l'intervalle d'amplitude , par exemple, . Puis, grace à sa parité, il est possible de réduire l'intervalle d'étude de moitié, à savoir étudier les variations de uniquement sur l'intervalle .
Donc :
Soit :
Mais comme , on en déduit que finalement :
Soit :
Comme , cela nous permet d'en conclure que :
Ainsi, sur l'intervalle la fonction est croissante et évolue de à .
De plus, on a , le théorème de nous assure de l'existance d'au moins un nombre réel tel que et . Afin de savoir si le nombre réel est unique, étudions . On a alors :
Soit :
En simplifiant par le terme on obtient :
Or, on sait que :
Donc :
Soit encore :
En développant :
Et encore :
D'où :
Donc :
Finalement :
Etudions le signe du numérateur, noté , de . Pour cela, posons . On a alors :
Le discriminant associé à ce trinôme est :
Par hypothèse, et sont deux nombres réels strictement positifs, donc . Ainsi le numérateur admet deux racines réelles distinctes que nous noterons et . Leurs expressions sont :
Soit :
Soit encore :
Donc, on constate que :
Or, on a poser , et de fait est clairement impossible. Puis, on a :
En effet, , donc il suffit d'étudier le signe du numérateur. Raisonnons par l'absurde. Pour cela, supposons donc que . Dans ce cas :
En développant :
Mais, par hypothese, et sont deux nombres réels strictement positifs. Donc ne peut être qu'une quantité positive. Donc, le fait d'aboutir à l'inégalité conduit à une contradiction (une absurdité). Ainsi, notre hypothèse initiale est fausse. On a donc :
Donc . On en déduit que et donc que . Ains le numérateur de ne s'annule qu'une seule fois.
Dit autrement, la dérivée seconde s'annule une, et une seule, fois sur l'intervale .
On constate alors qu'elle est de classe sur et qu'elle est paire.
La présence du terme nous invite à vérifier sa périodicité. La présence du carré sur le cosinus nous laisse penser qu'elle peut-être de période . Vérifions ceci. Soit un réel. On a alors :
Ainsi, effectivement, est périodique. La conséquence de cette périodicité est qu'il est possible d'étudier les variations de sur l'intervalle d'amplitude , par exemple, . Puis, grace à sa parité, il est possible de réduire l'intervalle d'étude de moitié, à savoir étudier les variations de uniquement sur l'intervalle .
Donc :
Soit :
Mais comme , on en déduit que finalement :
Soit :
Comme , cela nous permet d'en conclure que :
Ainsi, sur l'intervalle la fonction est croissante et évolue de à .
De plus, on a , le théorème de nous assure de l'existance d'au moins un nombre réel tel que et . Afin de savoir si le nombre réel est unique, étudions . On a alors :
Soit :
En simplifiant par le terme on obtient :
Or, on sait que :
Donc :
Soit encore :
En développant :
Et encore :
D'où :
Donc :
Finalement :
Etudions le signe du numérateur, noté , de . Pour cela, posons . On a alors :
Le discriminant associé à ce trinôme est :
Par hypothèse, et sont deux nombres réels strictement positifs, donc . Ainsi le numérateur admet deux racines réelles distinctes que nous noterons et . Leurs expressions sont :
Soit :
Soit encore :
Donc, on constate que :
Or, on a poser , et de fait est clairement impossible. Puis, on a :
En effet, , donc il suffit d'étudier le signe du numérateur. Raisonnons par l'absurde. Pour cela, supposons donc que . Dans ce cas :
En développant :
Mais, par hypothese, et sont deux nombres réels strictement positifs. Donc ne peut être qu'une quantité positive. Donc, le fait d'aboutir à l'inégalité conduit à une contradiction (une absurdité). Ainsi, notre hypothèse initiale est fausse. On a donc :
Donc . On en déduit que et donc que . Ains le numérateur de ne s'annule qu'une seule fois.
Dit autrement, la dérivée seconde s'annule une, et une seule, fois sur l'intervale .
Question 2
Soit la primitive de qui s'annule en . Déterminer .
Correction
La fonction est définie par :
Pour tout réel, on sait que :
Donc, on en déduit que :
Soit un nombre réel strictement positif. Dans ce cas, on a :
Soit, avec et deux constantes réelles :
Donc :
Par passage à la limite lorsque , on constate que :
Le théorème de l'encadrement nous permet de conclure que, finalement, on a :
Pour tout réel, on sait que :
Donc, on en déduit que :
Soit un nombre réel strictement positif. Dans ce cas, on a :
Soit, avec et deux constantes réelles :
Donc :
Par passage à la limite lorsque , on constate que :
Le théorème de l'encadrement nous permet de conclure que, finalement, on a :
Question 3
Exprimer sur .
Correction
On cherche à exprimer :
Commençons par chercher :
En calculant , on constate que :
Soit :
Par application des règles de , on va poser le changement de variable . Ainsi :
Puis :
Soit :
Donc :
Soit encore :
Posons , dans ce cas, on obtient :
Lorsque la nombre réel est strictement positif on a (avec ) :
Donc, comme , on en déduit que :
Comme , on a alors :
Mais, nous avion initialement posé , donc :
Que nous écrirons sous la forme équivalente :
Ainsi :
La valeur est une valeur importante car , et que . On a alors :
La fonction admet un axe de symétrie en car . En effet, on sait que et donc et de fait on a automatiquement . Ainsi, on en déduit que :
Donc, pour , écrivons que :
Soit :
Nous allons ramener, dans cette dernière intégrale, la borne inférieure à zéro. Pour cela, posons . Dans ce cas on a :
Puis, lorsque on , ensuite lorsque on . Donc :
De fait, cela nous donne :
Et donc est périodique. Il nous suffit d'exprimer sur l'intervalle . C'est donc la présence du terme qui va nous guider selon l'expression trouvée précédemment :
Soit :
Soit encore :
D'où :
Donc :
Finalement :
On peut écrire :
Dans ce cas et de fait . Ce qui nous permet d'écrire que :
Finalement, on obtient :
On en déduit immédiatement que :
Dans ce cas on a :
Soit :
Lorsque on sait que . Donc :
Or, lorsque on a et de fait . Donc on a :
Ce qui nous donne :
Soit :
On a alors :
Finalement :
On rappelle que :
D'après l'étude on a :
Dans ce cas on a :
Avec :
.
Et aussi :
.
Graphiquement, ceci se vérifie parfaitement. Voici la courbe représentative de sur l'intervalle :
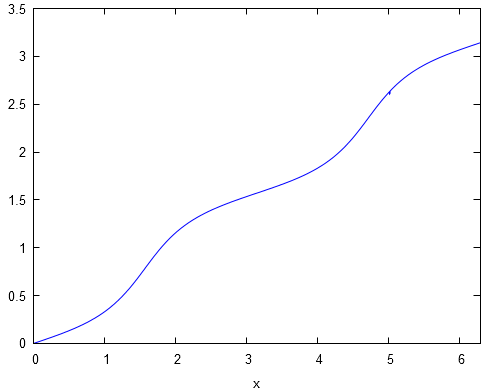
Commençons par chercher :
En calculant , on constate que :
Soit :
Par application des règles de , on va poser le changement de variable . Ainsi :
Puis :
Soit :
Donc :
Soit encore :
Posons , dans ce cas, on obtient :
Lorsque la nombre réel est strictement positif on a (avec ) :
Donc, comme , on en déduit que :
Comme , on a alors :
Mais, nous avion initialement posé , donc :
Que nous écrirons sous la forme équivalente :
Ainsi :
La valeur est une valeur importante car , et que . On a alors :
La fonction admet un axe de symétrie en car . En effet, on sait que et donc et de fait on a automatiquement . Ainsi, on en déduit que :
Donc, pour , écrivons que :
Soit :
Nous allons ramener, dans cette dernière intégrale, la borne inférieure à zéro. Pour cela, posons . Dans ce cas on a :
Puis, lorsque on , ensuite lorsque on . Donc :
De fait, cela nous donne :
Et donc est périodique. Il nous suffit d'exprimer sur l'intervalle . C'est donc la présence du terme qui va nous guider selon l'expression trouvée précédemment :
Soit :
Soit encore :
D'où :
Donc :
Finalement :
On peut écrire :
Dans ce cas et de fait . Ce qui nous permet d'écrire que :
Finalement, on obtient :
On en déduit immédiatement que :
Dans ce cas on a :
Soit :
Lorsque on sait que . Donc :
Or, lorsque on a et de fait . Donc on a :
Ce qui nous donne :
Soit :
On a alors :
Finalement :
On rappelle que :
D'après l'étude on a :
Dans ce cas on a :
Avec :
.
Et aussi :
.
Graphiquement, ceci se vérifie parfaitement. Voici la courbe représentative de sur l'intervalle :

Question 4
Calculer .
Correction
On a :
Donc :
Il s'agit de la fonction pour , avec et . Donc :
Finalement :
A l'aide d'un logiciel de calcul formel, on trouve que :

Ce qui est en parfait accord avec nos résultats issus de l'étude générale conduite dans ce problème.
Donc :
Il s'agit de la fonction pour , avec et . Donc :
Finalement :
A l'aide d'un logiciel de calcul formel, on trouve que :

Ce qui est en parfait accord avec nos résultats issus de l'étude générale conduite dans ce problème.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.