Champagne ! - Exercice 1

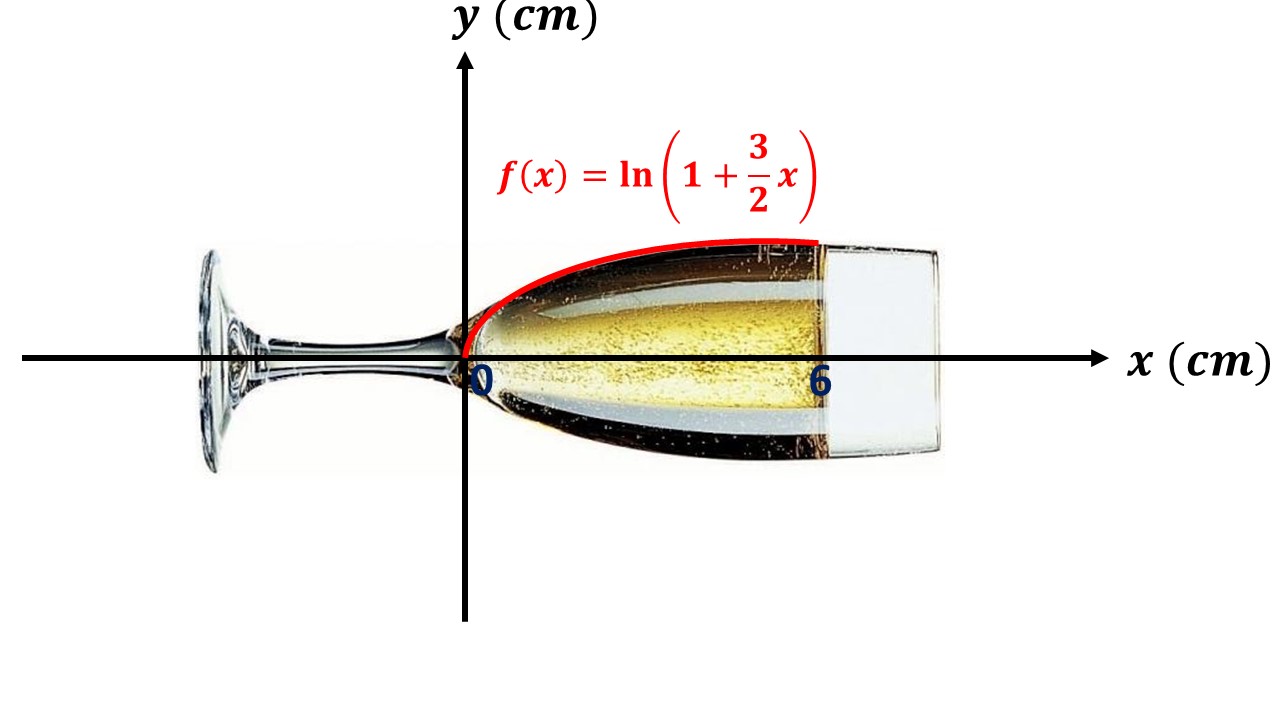
La valeur exacte, en $$cm^3$$ de $$\mathcal{V}$$ est donnée par :
$$\mathcal{V} = \pi \int_{0}^{6} f^2(x) \, dx \,\,\,\,\, \Longleftrightarrow \,\,\,\,\, \mathcal{V} = \pi \int_{0}^{6} \ln^2 \left( 1 + \dfrac{3}{2} x\right) \, dx$$
Que nous allons réécrire comme :
$$\mathcal{V} = \pi \int_{0}^{6} 1 \times \ln^2 \left( 1 + \dfrac{3}{2} x\right) \, dx \,\,\,\,\, \Longleftrightarrow \,\,\,\,\, \dfrac{\mathcal{V}}{\pi} = \int_{0}^{6} 1 \times \ln^2 \left( 1 + \dfrac{3}{2} x\right) \, dx$$
En utilisant la technique de l'intégration par parties, on obtient :
$$\dfrac{\mathcal{V}}{\pi} = \left[ x \ln^2 \left( 1 + \dfrac{3}{2} x\right)\right]_{0}^{6} - \int_{0}^{6} x \times 2\times \dfrac{\dfrac{3}{2}}{1+ \dfrac{3}{2}x} \times \ln \left( 1 + \dfrac{3}{2} x \right) \, dx$$
Soit encore :
$$\dfrac{\mathcal{V}}{\pi} = 6 \ln^2 \left( 1 + \dfrac{3}{2} \times 6\right) - \int_{0}^{6} \dfrac{3x}{1+\dfrac{3}{2}x}\ln \left( 1 + \dfrac{3}{2} x\right) \, dx$$
Ce qui nous donne :
$$\dfrac{\mathcal{V}}{\pi} = 6 \ln^2 ( 10 ) - 2 \int_{0}^{6} \dfrac{3x}{2+3x} \times \ln \left( 1 + \dfrac{3}{2} x\right) \, dx$$
Écrivons donc :
$$\dfrac{\mathcal{V}}{2\pi} = 3 \ln^2 ( 10 ) - \int_{0}^{6} \dfrac{3x+2-2}{3x+2} \times \ln \left( 1 + \dfrac{3}{2} x\right) \, dx$$
On obtient alors :
$$\dfrac{\mathcal{V}}{2\pi} = 3 \ln^2 ( 10 ) - \int_{0}^{6} \left( \dfrac{3x+2}{3x+2} - \dfrac{2}{3x+2} \right) \times \ln \left( 1 + \dfrac{3}{2} x\right) \, dx$$
Soit encore :
$$\dfrac{\mathcal{V}}{2\pi} = 3 \ln^2 ( 10 ) - \int_{0}^{6} \left( 1 - \dfrac{2}{3x+2} \right) \times \ln \left( 1 + \dfrac{3}{2} x\right) \, dx$$
Ce qui nous donne :
$$\dfrac{\mathcal{V}}{2\pi} = 3 \ln^2 ( 10 ) - \int_{0}^{6} 1 \times \ln \left( 1 + \dfrac{3}{2} x\right) \, dx+ 2 \int_{0}^{6} \dfrac{1}{3x+2} \times \ln \left( 1 + \dfrac{3}{2} x\right) \, dx$$
D'où :
$$\dfrac{\mathcal{V}}{2\pi} = 3 \ln^2 ( 10 ) - \int_{0}^{6} 1 \times \ln \left( 1 + \dfrac{3}{2} x\right) \, dx + \int_{0}^{6} \dfrac{1}{1+\dfrac{3}{2}x} \times \ln \left( 1 + \dfrac{3}{2} x\right) \, dx$$
Qui va encore s'écrire :
$$\dfrac{\mathcal{V}}{2\pi} = 3 \ln^2 ( 10 ) - \int_{0}^{6} 1 \times \ln \left( 1 + \dfrac{3}{2} x\right) \, dx + \dfrac{2}{3} \int_{0}^{6} \dfrac{\dfrac{3}{2}}{1+\dfrac{3}{2}x} \times \ln \left( 1 + \dfrac{3}{2} x\right) \, dx$$
Et encore :
$$\dfrac{\mathcal{V}}{2\pi} = 3 \ln^2 ( 10 ) - \int_{0}^{6} 1 \times \ln \left( 1 + \dfrac{3}{2} x\right) \, dx + \dfrac{1}{3} \int_{0}^{6} 2\times \dfrac{\dfrac{3}{2}}{1+\dfrac{3}{2}x} \times \ln \left( 1 + \dfrac{3}{2} x\right) \, dx$$
La seconde intégrale s'intègre directement :
$$\dfrac{\mathcal{V}}{2\pi} = 3 \ln^2 ( 10 ) - \int_{0}^{6} 1 \times \ln \left( 1 + \dfrac{3}{2} x\right) \, dx + \dfrac{1}{3}\left[ \ln^2 \left( 1 + \dfrac{3}{2} x\right) \right]_{0}^{6}$$
Comme $$\ln(1) =0$$, on en déduit que :
$$\dfrac{\mathcal{V}}{2\pi} = 3 \ln^2 ( 10 ) - \int_{0}^{6} 1 \times \ln \left( 1 + \dfrac{3}{2} x\right) \, dx + \dfrac{1}{3} \ln^2 \left( 1 + \dfrac{3}{2} \times 6 \right)$$
Soit encore :
$$\dfrac{\mathcal{V}}{2\pi} = 3 \ln^2 ( 10 ) - \int_{0}^{6} 1 \times \ln \left( 1 + \dfrac{3}{2} x\right) \, dx + \dfrac{1}{3} \ln^2 \left( 10 \right)$$
D'où :
$$\dfrac{\mathcal{V}}{2\pi} = \dfrac{10}{3} \ln^2 ( 10 ) - \int_{0}^{6} 1 \times \ln \left( 1 + \dfrac{3}{2} x\right) \, dx$$
Puis, en effectuant une nouvelle intégration par parties, on peut écrire que :
$$\dfrac{\mathcal{V}}{2\pi} = \dfrac{10}{3} \ln^2 ( 10 ) - \left[ x \ln \left( 1 + \dfrac{3}{2} x\right) \right]_{0}^{6} + \int_{0}^{6} x \times \dfrac{\dfrac{3}{2}}{1 + \dfrac{3}{2} x} \, dx$$
Soit :
$$\dfrac{\mathcal{V}}{2\pi} = \dfrac{10}{3} \ln^2 ( 10 ) - 6 \ln \left( 1 + \dfrac{3}{2} \times 6 \right) + \int_{0}^{6} x \times \dfrac{\dfrac{3}{2}}{\dfrac{2}{2}+\dfrac{3}{2} x} \, dx$$
Qui prend la forme suivante :
$$\dfrac{\mathcal{V}}{2\pi} = \dfrac{10}{3} \ln^2 ( 10 ) - 6 \ln \left( 10 \right) + \int_{0}^{6} \dfrac{3x}{2+3x} \, dx$$
Donnons lui la forme suivante :
$$\dfrac{\mathcal{V}}{2\pi} =\dfrac{10}{3} \ln^2 ( 10 ) - 6 \ln \left( 10 \right) + \int_{0}^{6} \dfrac{2+3x-2}{2+3x} \, dx$$
Pour décomposer ainsi :
$$\dfrac{\mathcal{V}}{2\pi} = \dfrac{10}{3} \ln^2 ( 10 ) - 6 \ln \left( 10 \right) + \int_{0}^{6} \left( 1 - \dfrac{2}{2+3x} \right) \, dx$$
Ce qui nous donne :
$$\dfrac{\mathcal{V}}{2\pi} = \dfrac{10}{3} \ln^2 ( 10 ) - 6 \ln \left( 10 \right) + \int_{0}^{6} 1 \, dx - \int_{0}^{6} \dfrac{2}{2+3x} \, dx$$
Soit encore :
$$\dfrac{\mathcal{V}}{2\pi} = \dfrac{10}{3} \ln^2 ( 10 ) - 6 \ln \left( 10 \right) + \left[ x\right] _{0}^{6} - \int_{0}^{6} \dfrac{1}{1+\dfrac{3}{2}x} \, dx$$
On a donc :
$$\dfrac{\mathcal{V}}{2\pi} = \dfrac{10}{3} \ln^2 ( 10 ) - 6 \ln \left( 10 \right) + 6 - \dfrac{2}{3} \int_{0}^{6} \dfrac{\dfrac{3}{2}}{1+\dfrac{3}{2}x} \, dx$$
D'où :
$$\dfrac{\mathcal{V}}{2\pi} = \dfrac{10}{3} \ln^2 ( 10 ) - 6 \ln \left( 10 \right) + 6 - \dfrac{2}{3} \left[ \ln\left( 1+\dfrac{3}{2}x \right) \right] _{0}^{6}$$
On trouve donc :
$$\dfrac{\mathcal{V}}{2\pi} = \dfrac{10}{3} \ln^2 ( 10 ) - 6 \ln \left( 10 \right) + 6 - \dfrac{2}{3} \ln\left( 1+\dfrac{3}{2} \times 6 \right)$$
Soit :
$$\dfrac{\mathcal{V}}{2\pi} = \dfrac{10}{3} \ln^2 ( 10 ) - 6 \ln \left( 10 \right) + 6 - \dfrac{2}{3} \ln( 10 )$$
D'où :
$$\dfrac{\mathcal{V}}{2\pi} = \dfrac{10}{3} \ln^2 ( 10 ) - \dfrac{20}{3} \ln \left( 10 \right) + 6$$
En factorisant par $$\dfrac{10}{3} \ln^2 ( 10 )$$, on trouve que :
$$\dfrac{\mathcal{V}}{2\pi} = \dfrac{10}{3} \ln ( 10 ) \left( \ln ( 10 ) - 2 \right) + 6$$
Ou encore en factorisant par $$2$$ :
$$\dfrac{\mathcal{V}}{2\pi} = 2\left( \dfrac{5}{3} \ln ( 10 ) \left( \ln ( 10 ) - 2 \right) + 3 \right)$$
Finalement, on trouve que :
$$\boxed{\mathcal{V} = 4 \pi \left( \dfrac{5}{3} \ln ( 10 ) \left( \ln ( 10 ) - 2 \right) + 3 \right) \,\, cm^3}$$

La valeur approchée, au millième de $$cm^3$$, de $$\mathcal{V}$$ est :
$$\boxed{\mathcal{V} \simeq 52,291 \,\, cm^3 }$$