Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Pour débuter - Exercice 1
1 h
90
Question 1
Effectuer la division euclidienne de par .
Correction
On a la séquence calculatoire suivante :
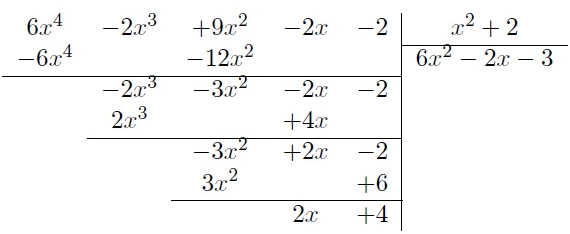
Donc, on en déduit que :
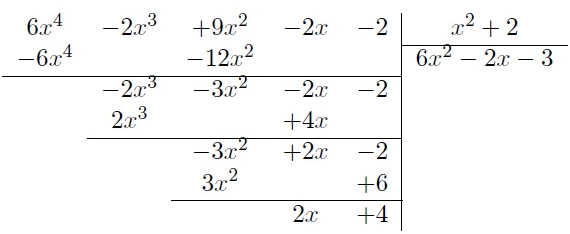
Donc, on en déduit que :
Question 2
Effectuer la division euclidienne de par .
Correction
On a la séquence calculatoire suivante :
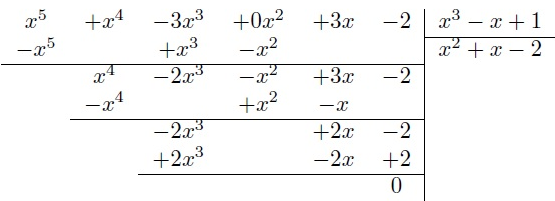
Donc, on en déduit que :
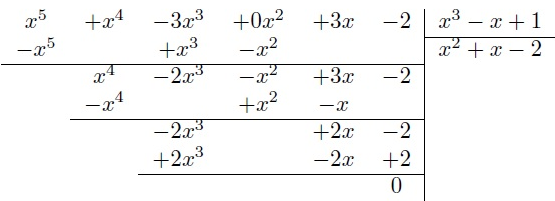
Donc, on en déduit que :
Question 3
Effectuer la division euclidienne de par .
Correction
On a la séquence calculatoire suivante :
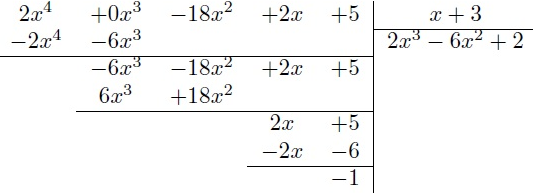
Donc, on en déduit que :
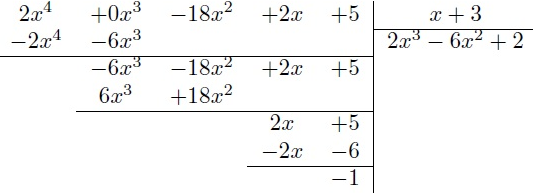
Donc, on en déduit que :
Question 4
Déduire, de la question précédente, la décomposition en éléments simples de la fraction rationnelle suivante :
Correction
D'après la question précédente, on a :
Soit, pour :
En scindant en deux parties :
Soit encore :
Finalement, on en déduit que :
Soit, pour :
En scindant en deux parties :
Soit encore :
Finalement, on en déduit que :
Question 5
Factoriser, dans , le polynôme suivant : .
Correction
Nous allons utiliser la technique de la racine évidente, puis une méthode de factorisation très efficace, et rapide, la .
Testons la valeur . On a alors :
.
Ainsi, est une racine évidente.
La méthode de Horner consiste à construire un tableau de trois lignes. Dans la ligne du haut, nous allons indiquer les coefficients du , et dans l'ordre des puissances décroissantes. Il faudra indiquer un si une puissance n'est pas représentée dans le polynôme.
Dans la deuxième ligne, première colonne, on indiquera trouvée.
Puis dans la troisième ligne apparaitrons , tel que . Avec la condition .
Dans notre cas ce qui implique que .
On commence par recopier le premier coefficient (en bleu) du polynôme à factoriser (celui de la première ligne) dans la troisième ligne en dessous dans la même colonne (en rouge). Puis, on multiplie ce coefficient par la racine évidente, et le résultat se note dans la case se trouvant dans la deuxième ligne et dans la colonne suivante. A ce stade, on additionne les nombres se trouvant dans les cases des deux première ligne, et le résultat de cette addition s'inscrit la la même colonne mais dans la dernière ligne, donc en rouge. Et on recommence la même procédure avec ce nouveau nombre. Lorsque la procédure se termine, on doit obligatoirement trouver dans la dernière case, à la croisée de la dernière colonne et de la dernière ligne.
On a alors :
Les trois coefficients en rouge se trouvant dans la troisième et dernière ligne forment le polynôme selon les puissances décroissantes.
On a donc :
A ce stade, nous pouvons écrire que :
Essayons de factoriser, dans , le polynôme . Le discriminant associé vaut :
On en déduit que n'est pas factorisable dans .
Finalement, la factorisation de , dans , est donnée par l'expression suivante :
Testons la valeur . On a alors :
.
Ainsi, est une racine évidente.
La méthode de Horner consiste à construire un tableau de trois lignes. Dans la ligne du haut, nous allons indiquer les coefficients du , et dans l'ordre des puissances décroissantes. Il faudra indiquer un si une puissance n'est pas représentée dans le polynôme.
Dans la deuxième ligne, première colonne, on indiquera trouvée.
Puis dans la troisième ligne apparaitrons , tel que . Avec la condition .
Dans notre cas ce qui implique que .
On commence par recopier le premier coefficient (en bleu) du polynôme à factoriser (celui de la première ligne) dans la troisième ligne en dessous dans la même colonne (en rouge). Puis, on multiplie ce coefficient par la racine évidente, et le résultat se note dans la case se trouvant dans la deuxième ligne et dans la colonne suivante. A ce stade, on additionne les nombres se trouvant dans les cases des deux première ligne, et le résultat de cette addition s'inscrit la la même colonne mais dans la dernière ligne, donc en rouge. Et on recommence la même procédure avec ce nouveau nombre. Lorsque la procédure se termine, on doit obligatoirement trouver dans la dernière case, à la croisée de la dernière colonne et de la dernière ligne.
On a alors :
Les trois coefficients en rouge se trouvant dans la troisième et dernière ligne forment le polynôme selon les puissances décroissantes.
On a donc :
A ce stade, nous pouvons écrire que :
Essayons de factoriser, dans , le polynôme . Le discriminant associé vaut :
On en déduit que n'est pas factorisable dans .
Finalement, la factorisation de , dans , est donnée par l'expression suivante :
Question 6
Factoriser, dans , le polynôme suivant : .
Correction
D'après la question précédente, on sait que .
De plus, le discriminant associé au polynôme du second degré est . On a alors, avec :
D'où :
Finalement, la factorisation de , dans , est donnée par l'expression suivante :
De plus, le discriminant associé au polynôme du second degré est . On a alors, avec :
D'où :
Finalement, la factorisation de , dans , est donnée par l'expression suivante :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.