Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
On divise encore, on décompose et on intègre ! - Exercice 1
50 min
75
Un exemple simple pour vérifier si l'on sait correctement réaliser une division euclidienne selon les puissances décroissantes de l'indéterminée.
Question 1
Soit une indéterminée.
On considère et deux polynômes à coefficients réels, tels que :
et
On supposera que est non nul.
On notera par le nombre complexe suivant :
On considère et deux polynômes à coefficients réels, tels que :
et
On supposera que est non nul.
On notera par le nombre complexe suivant :
Effectuer la division euclidienne de par selon les puissances décroissantes de .
Correction
On a la séquence calculatoire suivante :
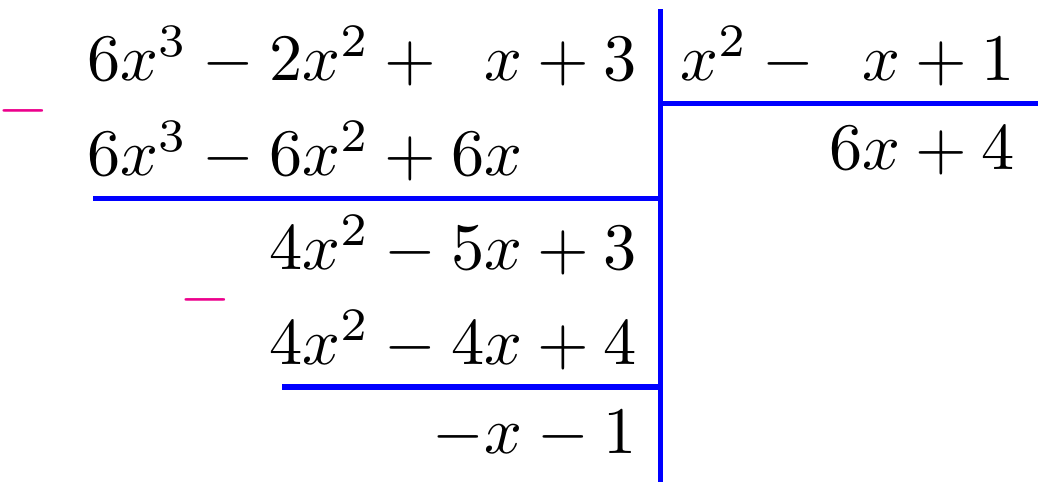
Ce qui nous permet d'écrire que :
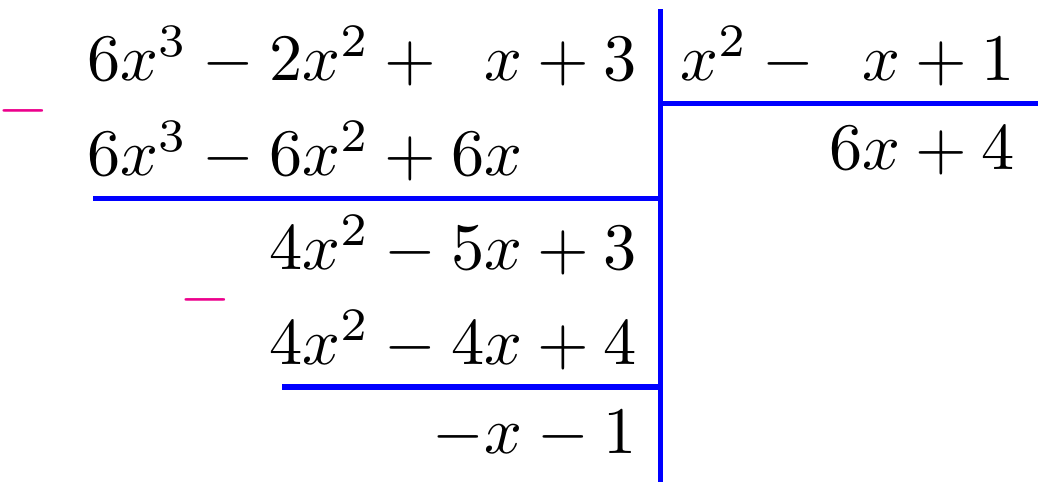
Ce qui nous permet d'écrire que :
Question 2
Dans , décomposer en éléments simples la fraction rationnelle suivante :
Correction
On a :
Soit encore :
Comme est supposé non nul, on a :
Donc :
On doit donc décomposer en éléments simples, dans , la fraction rationnelle suivante :
Le discriminant associé au polynôme est . Donc n'est pas factorisable dans .
Finalement, on trouve que :
Soit encore :
Comme est supposé non nul, on a :
Donc :
On doit donc décomposer en éléments simples, dans , la fraction rationnelle suivante :
Le discriminant associé au polynôme est . Donc n'est pas factorisable dans .
Finalement, on trouve que :
Question 3
Dans , décomposer en éléments simples la fraction rationnelle suivante :
Correction
D'après la question précédente, on sait que :
On doit donc décomposer en éléments simples, dans , la fraction rationnelle suivante :
Le discriminant associé au polynôme est . Donc est factorisable dans . Les racines de sont, avec :
Donc :
D'où :
Ainsi :
La décomposition en éléments simples est donnée par l'expression :
En réduisant au même dénominateur, on obtient :
Donc, par identification, on trouve que et . Donc et de fait . Donc :
Soit :
Soit encore :
On en déduit que :
Ainsi :
Donc, la décomposition en éléments simples, dans , de la fraction rationnelle est donnée par :
Finalement, on obtient la décomposition en éléments simples, dans , de la fraction rationnelle suivante :
On doit donc décomposer en éléments simples, dans , la fraction rationnelle suivante :
Le discriminant associé au polynôme est . Donc est factorisable dans . Les racines de sont, avec :
Donc :
D'où :
Ainsi :
La décomposition en éléments simples est donnée par l'expression :
En réduisant au même dénominateur, on obtient :
Donc, par identification, on trouve que et . Donc et de fait . Donc :
Soit :
Soit encore :
On en déduit que :
Ainsi :
Donc, la décomposition en éléments simples, dans , de la fraction rationnelle est donnée par :
Finalement, on obtient la décomposition en éléments simples, dans , de la fraction rationnelle suivante :
Question 4
Déterminer l'expression des primitives de .
On rappelle que si est une fonction dérivable, on a :
On rappelle que si est une fonction dérivable, on a :
Correction
On a :
Soit :
Ou encore :
Ce qui nous donne :
Ceci prend également la forme suivante :
On a aussi :
De manière strictement équivalente :
Soit encore :
En forçant la factorisation par au dénominateur du dernier terme, on trouve :
Donc :
Qui peut également prendre la forme suivante :
Ou encore :
Qui est aussi :
En primitivant, on obtient, avec :
La primitivation étant linéaire, on a alors :
En sortant les constantes, on trouve que :
Donc :
Finalement, on trouve que :
Soit :
Ou encore :
Ce qui nous donne :
Ceci prend également la forme suivante :
On a aussi :
De manière strictement équivalente :
Soit encore :
En forçant la factorisation par au dénominateur du dernier terme, on trouve :
Donc :
Qui peut également prendre la forme suivante :
Ou encore :
Qui est aussi :
En primitivant, on obtient, avec :
La primitivation étant linéaire, on a alors :
En sortant les constantes, on trouve que :
Donc :
Finalement, on trouve que :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.