Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Décomposition en éléments simple dans - Exercice 2
30 min
50
Une décomposition en éléments simples dans .
Question 1
Soit une indéterminée.
Soit la fraction rationnelle suivante :
On note par le nombre complexe imaginaire pur tel que et on notera par le nombre complexe suivant :
Soit la fraction rationnelle suivante :
On note par le nombre complexe imaginaire pur tel que et on notera par le nombre complexe suivant :
Décomposer en éléments simples dans .
Correction
La fraction rationnelle est sous sa forme irréductible. Et, dans , on a :
De plus, le degré du dénominateur étant inférieur à celui du numérateur, le partie entière de est nulle. La décomposition de en éléments simples, dans , est donc :
Cependant, la fraction rationnelle proposée appartient à , donc est inchangée par le (on remplace tous les coefficients par leurs conjugués), d'où :
On en déduit immédiatement, par unicité de la décomposition, que :
Afin de faciliter la détermination des coefficients , et , on va poser :
Ainsi, avec , on a :
Ce qui implique que :
On peut alors écrire que :
Comme est un pôle , on va effectuer la division euclidienne de par suivant les valeurs croissantes de jusqu'à . On a alors :
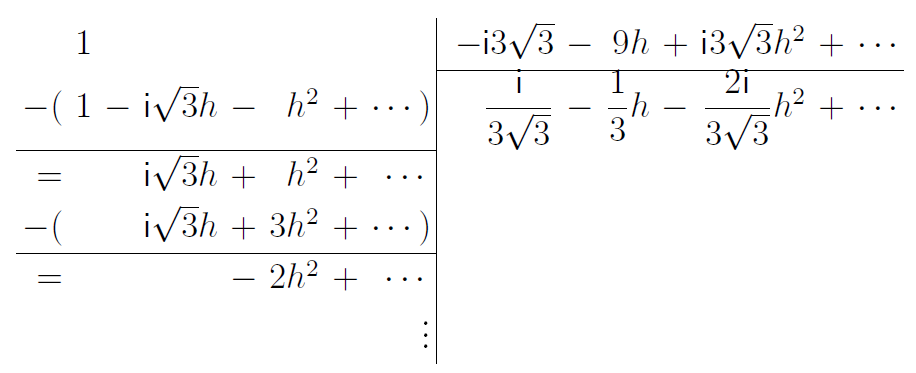
On obtient alors les trois coefficients complexes recherchés :
On en déduit alors que :
Finalement la décomposition de en éléments simples dans est :
De plus, le degré du dénominateur étant inférieur à celui du numérateur, le partie entière de est nulle. La décomposition de en éléments simples, dans , est donc :
Cependant, la fraction rationnelle proposée appartient à , donc est inchangée par le (on remplace tous les coefficients par leurs conjugués), d'où :
On en déduit immédiatement, par unicité de la décomposition, que :
Afin de faciliter la détermination des coefficients , et , on va poser :
Ainsi, avec , on a :
Ce qui implique que :
On peut alors écrire que :
Comme est un pôle , on va effectuer la division euclidienne de par suivant les valeurs croissantes de jusqu'à . On a alors :
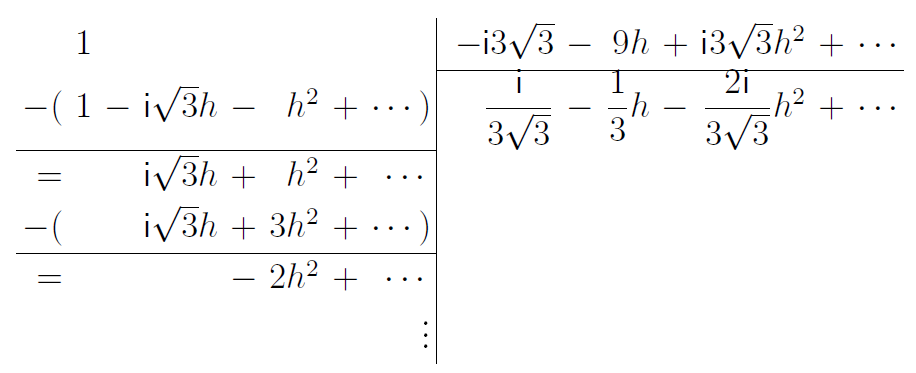
On obtient alors les trois coefficients complexes recherchés :
On en déduit alors que :
Finalement la décomposition de en éléments simples dans est :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.