Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Autour des racines n-ième des nombres complexes - Exercice 3

20 min
35
Soit nn un nombre entier naturel non nul. Soit aa un nombre complexe quelconque, qui a pour forme exponentielle a=ρ ei θa = \rho \, e^{i \, \theta}. Dans ce cas ρ=∣ a ∣>0\rho = |\,a\,| > 0 est la module de aa et θ=arg⁡(a)∈R\theta = \arg(a) \in \mathbb{R}.
Soit kk un entier naturel, qui peut prendre uniquement nn valeurs, tel que 0⩽k⩽n−10 \leqslant k \leqslant n-1. On appelle racines  n−ieˋmes  de  a{\color{red}{racines \,\, n-ièmes} \,\, de \,\, a} les nn nombres complexes zkz_k qui sont solution de l'équation complexe zn=az^n = a et qui s'écrivent sous la forme suivante :
zk=ρn ei θ+2kπn=ρn (cos⁡(θ+2kπn)+i sin⁡(θ+2kπn))z_k = \sqrt[n]{\rho} \, e^{i \, \frac{\theta + 2k\pi}{n}} = \sqrt[n]{\rho} \, \left(\cos\left(\dfrac{\theta + 2k\pi}{n}\right) + i \, \sin\left(\dfrac{\theta + 2k\pi}{n}\right)\right)
D'un point de vue géométrique, dans le plan complexe, les images des nn nombres complexes zkz_k forment un polygone régulier à nn cotés, inscrit dans un cercle centré sur l'origine et de rayon rr qui vaut : r=∣ a ∣nr = \sqrt[n]{|\,a\,|}.
Si a=1a=1 alors on parle de racines  n−ieˋmes  de  l′uniteˊ{\color{red}{racines \,\, n-ièmes} \,\, de \,\, l'unité}, et on les note ωk\omega_k. Dans ce cas particulier elles sont solutions de l'équation complexe zn=1z^n=1, et comme 1=ei 01 = e^{i\, 0}, elles ont donc la forme suivante :
ωk=ei 2kπn=cos⁡(2kπn)+i sin⁡(2kπn)\omega_k = e^{i \, \frac{2k\pi}{n}} = \cos\left(\dfrac{2k\pi}{n}\right) + i \, \sin\left(\dfrac{ 2k\pi}{n}\right)
Il est vraiment important de savoir déterminer des racines n-ièmes de nombres complexes quelconques.
Question 1

Résoudre l'équation complexe z5=iz^5 = i.

Correction
Comme i=1 eiπ2i = 1 \, e^{i \frac{\pi}{2}}, on on déduit que :
a=0+1 i=1 eiπ2a = 0 + 1 \, i = 1 \, e^{i \frac{\pi}{2}}
  • Soit a=reiθa=re^{i\theta} avec r>0r>0 et θ∈[0;2π[\theta \in \left[0;2\pi \right[ un nombre complexe non nul et soit nn entier naturel non nul.
    Le nombre complexe aa admet nn racines nième distinctes définies par : zk=(r)1nei(θ+2kπn)z_k={\left(r\right)}^{\frac{1}{n}}e^{i\left(\frac{\theta +2k\pi }{n}\right)} où k∈[[0;n−1]]k \in\left[\left[0;n-1\right]\right]
Les solutions complexes zkz_k de l'équation proposée z5=iz^5 = i, avec k={0 ; 1 ; 2 ; 3 ; 4}k = \left\{ 0\,;\,1\,;\,2\,;\,3\,;\,4 \right\} , sont donc données par :
zk=15 eiπ2+2kπ5=1 ei(π10+2kπ5)=ei(π10+2kπ5)z_k = \sqrt[5]{1} \, e^{i \frac{\frac{\pi}{2}+2k\pi}{5}} = 1 \, e^{i \left( \frac{\pi}{10} + \frac{2k\pi}{5} \right)} = e^{i \left( \frac{\pi}{10} + \frac{2k\pi}{5} \right)}
Nous recherchons donc les racines cinquième du nombre complexe a=ia=i. On a alors les solutions suivantes :
   ∙  si  k=0{\color{blue}{\,\,\, \bullet \,\, \mathrm{si} \,\, k = 0}}
Alors :
z0=eiπ10z_0 = e^{i \frac{\pi}{10}}
   ∙∙  si  k=1{\color{blue}{\,\,\, \bullet \bullet \,\, \mathrm{si} \,\, k = 1}}
Alors :
z1=eiπ10+2π5=eiπ10+4π10=eiπ+4π10=ei5π10=eiπ2=iz_1 = e^{i \frac{\pi}{10} + \frac{2\pi}{5}} = e^{i \frac{\pi}{10} + \frac{4\pi}{10}} = e^{i \frac{\pi + 4\pi}{10}} = e^{i \frac{5\pi}{10}} = e^{i \frac{\pi}{2}} = i
   ∙∙∙  si  k=2{\color{blue}{\,\,\, \bullet \bullet \bullet \,\, \mathrm{si} \,\, k = 2}}
Alors :
z2=eiπ10+4π5=eiπ10+8π10=eiπ+8π10=ei9π10z_2 = e^{i \frac{\pi}{10} + \frac{4\pi}{5}} = e^{i \frac{\pi}{10} + \frac{8\pi}{10}} = e^{i \frac{\pi + 8\pi}{10}} = e^{i \frac{9\pi}{10}}
   ∙∙∙∙  si  k=3{\color{blue}{\,\,\, \bullet \bullet \bullet \bullet\,\, \mathrm{si} \,\, k = 3}}
Alors :
z3=eiπ10+6π5=eiπ10+12π10=eiπ+12π10=ei13π10=e−i7π10z_3 = e^{i \frac{\pi}{10} + \frac{6\pi}{5}} = e^{i \frac{\pi}{10} + \frac{12\pi}{10}} = e^{i \frac{\pi + 12\pi}{10}} = e^{i \frac{13\pi}{10}} = e^{-i \frac{7\pi}{10}}
   ∙∙∙∙∙  si  k=4{\color{blue}{\,\,\, \bullet \bullet \bullet \bullet \bullet \,\, \mathrm{si} \,\, k = 4}}
Alors :
z4=eiπ10+8π5=eiπ10+16π10=eiπ+16π10=ei17π10=e−i3π10z_4 = e^{i \frac{\pi}{10} + \frac{8\pi}{5}} = e^{i \frac{\pi}{10} + \frac{16\pi}{10}} = e^{i \frac{\pi + 16\pi}{10}} = e^{i \frac{17\pi}{10}} = e^{-i \frac{3\pi}{10}}
Finalement, les solutions recherchées sont :
z=eiπ10   ou   z=i   ou   z=ei9π10   ou   z=e−i7π10   ou   z=e−i3π10{\color{red}{\boxed{ z = e^{i \frac{\pi}{10}} \,\,\, \mathrm{ou} \,\,\, z = i \,\,\, \mathrm{ou} \,\,\, z = e^{i \frac{9\pi}{10}} \,\,\, \mathrm{ou} \,\,\, z = e^{-i \frac{7\pi}{10}} \,\,\, \mathrm{ou} \,\,\, z = e^{-i \frac{3\pi}{10}}}}}
Question 2

Déterminer les racines cubiques de l'unité.

Correction
On s'intéresse à la résolution, dans C\mathbb{C}, de l'équation z3=1z^3 = 1. Cette équation s'écrit encore :
z3=1ei 0z^3 = 1 e^{i \, 0}
Les solutions de cette équations sont des nombres complexes, notés ωk\omega_k, avec k={0 ; 1 ; 2}k = \left\{ 0\,;\,1\,;\,2 \right\} , et qui s'écrivent :
   ∙  si  k=0{\color{blue}{\,\,\, \bullet \,\, \mathrm{si} \,\, k = 0}}
Alors :
ω0=ei 2×0×π3=ei 0=1\omega_0 = e^{i \, \frac{2\times 0 \times \pi}{3}} = e^{i \, 0} = 1
   ∙∙  si  k=1{\color{blue}{\,\,\, \bullet \bullet \,\, \mathrm{si} \,\, k = 1}}
Alors :
ω1=ei 2×1×π3=ei 2π3=cos⁡(2π3)+i sin⁡(2π3)=−12+i 32=−1+i 32\omega_1 = e^{i \, \frac{2 \times 1 \times \pi}{3}} = e^{i \, \frac{2\pi}{3}} = \cos\left(\dfrac{2\pi}{3}\right) + i \, \sin\left(\dfrac{ 2\pi}{3}\right) = - \dfrac{1}{2} + i \, \dfrac{\sqrt{3}}{2} = \dfrac{-1 + i \, \sqrt{3}}{2}
Il est d'usage de noter ω1=j\omega_1 = j.
   ∙∙∙  si  k=2{\color{blue}{\,\,\, \bullet \bullet \bullet \,\, \mathrm{si} \,\, k = 2}}
Alors :
ω2=ei 2×2×π3=ei 4π3=ei (6−2)π3=ei 2π−i 2π3=ei 2π×e−i 2π3=1×e−i 2π3=e−i 2π3\omega_2 = e^{i \, \frac{2 \times 2 \times \pi}{3}} = e^{i \, \frac{4\pi}{3}} = e^{i \, \frac{(6-2)\pi}{3}} = e^{i \, 2\pi - i\, \frac{2\pi}{3}} = e^{i \, 2\pi} \times e^{- i\, \frac{2\pi}{3}} = 1 \times e^{- i\, \frac{2\pi}{3}} = e^{- i\, \frac{2\pi}{3}}
Ce qui nous donne :
ω2=e−i 2π3=cos⁡(−2π3)+i sin⁡(−2π3)=cos⁡(2π3)−i sin⁡(2π3)=−12−i 32=−1−i 32=ω1‾=jˉ\omega_2 = e^{- i\, \frac{2\pi}{3}} = \cos\left(-\dfrac{2\pi}{3}\right) + i \, \sin\left(-\dfrac{ 2\pi}{3}\right) = \cos\left(\dfrac{2\pi}{3}\right) - i \, \sin\left(\dfrac{ 2\pi}{3}\right) = - \dfrac{1}{2} - i \, \dfrac{\sqrt{3}}{2} = \dfrac{-1 - i \, \sqrt{3}}{2} = \overline{\omega_1} = \bar{j}
On a montrer que ω2=ei 4π3\omega_2 = e^{i \, \frac{4\pi}{3}}. Donc :
ω2=(ei 2π3)2=ω12=j2\omega_2 = \left( e^{i \, \frac{2\pi}{3}} \right)^2 = \omega_1^2 = j^2
On a alors :
ω2=ω1‾=jˉ=j2\omega_2 = \overline{\omega_1} = \bar{j} = j^2.
Finalement, les solutions recherchées sont :
z=1   ou   z=j=−1+i 32   ou   z=j2=jˉ=−1−i 32{\color{red}{\boxed{ z = 1 \,\,\, \mathrm{ou} \,\,\, z = j = \dfrac{-1 + i \, \sqrt{3}}{2} \,\,\, \mathrm{ou} \,\,\, z = j^2 = \bar{j} = \dfrac{-1 - i \, \sqrt{3}}{2}}}}
Question 3

Déterminer la valeur de la somme des trois racines cubiques de l'unité.

Correction
On cherche la valeur de la somme S3S_3 suivante :
S3=ω0+ω1+ω2S_3 = \omega_0 + \omega_1 + \omega_2
A savoir :
S3=1+j+j2S_3 = 1 + j + j^2
Soit :
S3=1−12+i 32−12−i 32S_3 = 1 - \dfrac{1}{2} + i \, \dfrac{\sqrt{3}}{2} - \dfrac{1}{2} - i \, \dfrac{\sqrt{3}}{2}
En simplifiant, on obtient :
S3=1−12−12S_3 = 1 - \dfrac{1}{2} - \dfrac{1}{2}
Donc :
S3=1−1S_3 = 1 - 1
Finalement :
S3=1+j+j2=0{\color{red}{\boxed{ S_3 = 1 + j + j^2 = 0}}}
Question 4

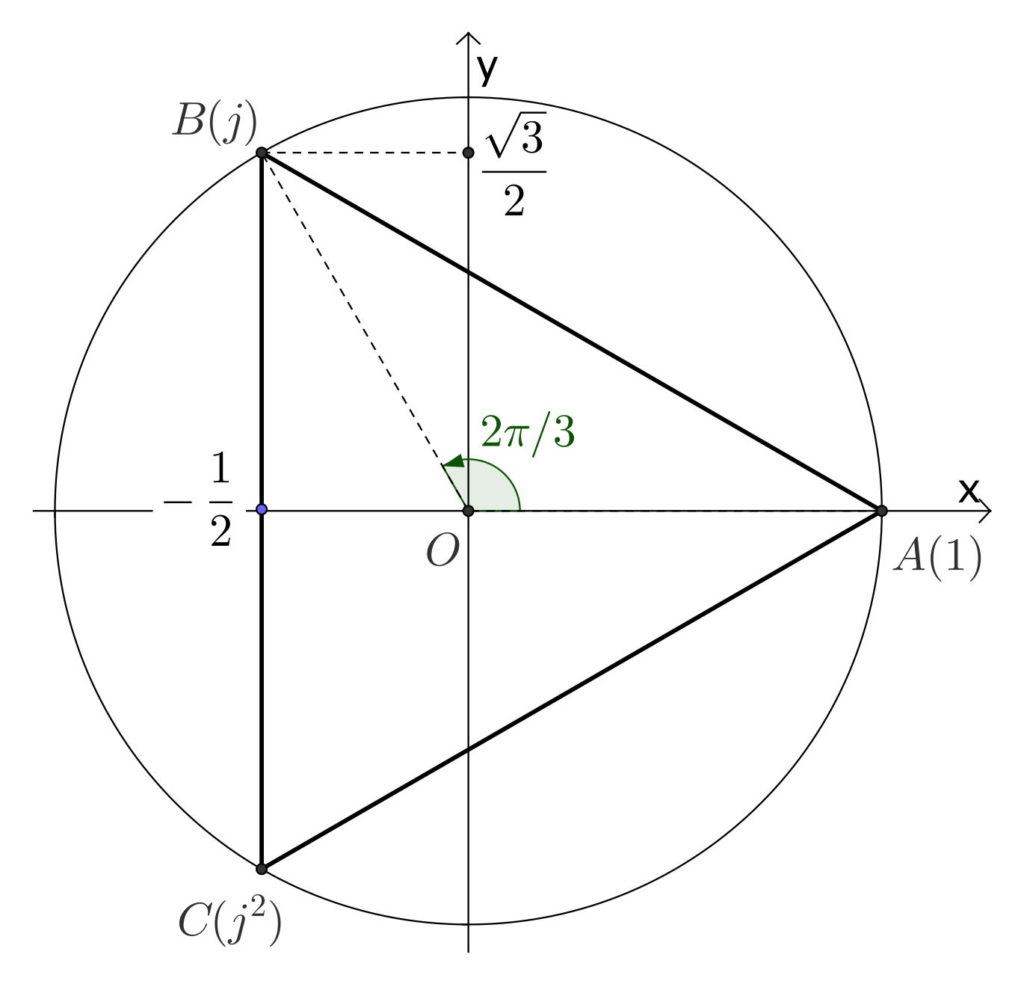
Proposer une construction géométrique associée aux trois racines cubiques de l'unité.

Correction
On a la construction géométrique suivante qui est associée au trois racines cubiques de l'unité :