Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Un peu de théorie (3) - Exercice 1
20 min
40
Toujours un exercice théorique.
Question 1
Soit et deux ensembles non vides.
Soit une application de vers .
On note par la bijection réciproque de .
On note par une partie de , et une partie de .
Le présence de l'écriture pourrait faire penser que serait une bijection, et que également. Ceci est vrai si s'applique à un élément d'un ensemble. Mais lorsque s'applique à un ensemble, par exemple, alors , appelé ensemble réciproque. En Aucun cas l'écriture ne suppose (ou induit) la nature bijective de l'application .
Pour préciser ceci, on considère l'application suivante :
On note par une partie de . L'ensemble réciproque , également noté et parfois aussi pour insister sur la nature ensembliste, est caractérisé par :
Et on peut y associer la figure suivante :
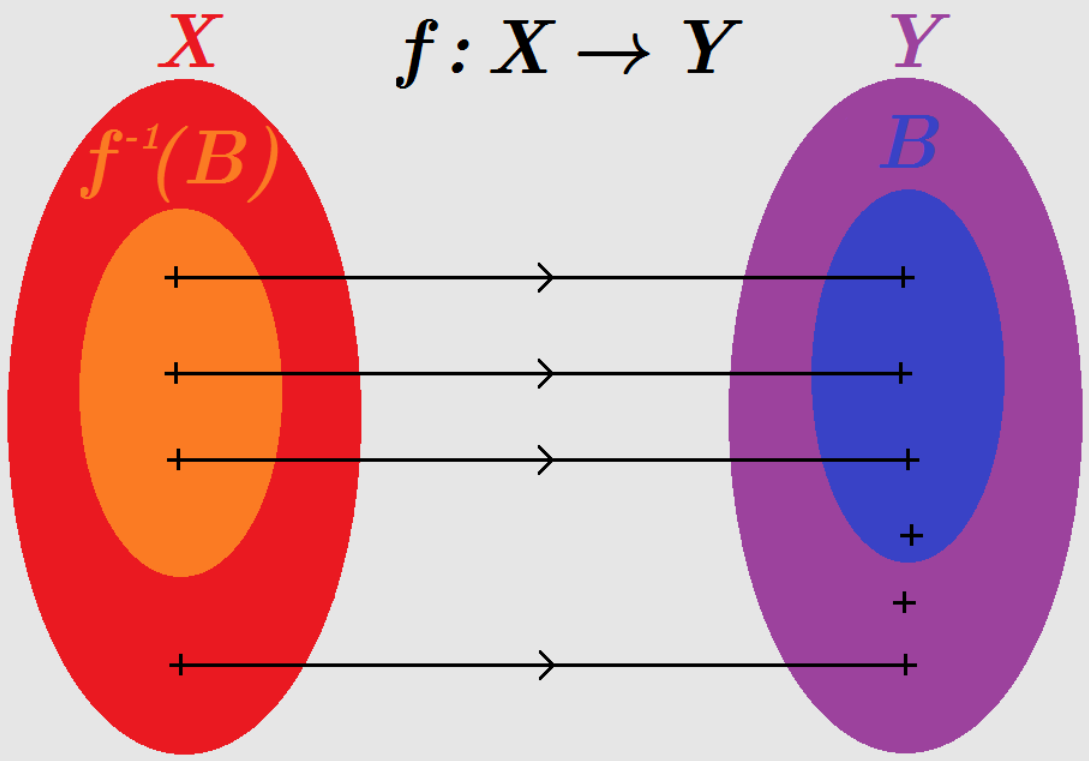
Soit une application de vers .
On note par la bijection réciproque de .
On note par une partie de , et une partie de .
Le présence de l'écriture pourrait faire penser que serait une bijection, et que également. Ceci est vrai si s'applique à un élément d'un ensemble. Mais lorsque s'applique à un ensemble, par exemple, alors , appelé ensemble réciproque. En Aucun cas l'écriture ne suppose (ou induit) la nature bijective de l'application .
Pour préciser ceci, on considère l'application suivante :
On note par une partie de . L'ensemble réciproque , également noté et parfois aussi pour insister sur la nature ensembliste, est caractérisé par :
Et on peut y associer la figure suivante :

Montrer que .
Correction
On rappelle que l'ensemble est inclus dans l'ensemble , qui se note se traduit par (en notant par un élément de l'ensemble ) l'assrtion suivante :
.
Soit un élément quelconque de l'ensemble . Ceci implique l'existence d'un élément appartenant à l'ensemble tel que . Or, et de fait .
On a donc prouvé que .
Ce qui prouve bien que .
.
Soit un élément quelconque de l'ensemble . Ceci implique l'existence d'un élément appartenant à l'ensemble tel que . Or, et de fait .
On a donc prouvé que .
Ce qui prouve bien que .
Question 2
Montrer que .
Correction
On suppose que . De fait, on a . Donc, on a immédiatement . Et comme nous avons supposé que , cela implique que .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.