Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Pour débuter : Injective, surjective et bijective - Exercice 2
45 min
65
Voici un premier exercice, constitué de question classiques (donc pédagogiques), pour s'habituer à ces nouvelles notions.
Question 1
Soit le nombre complexe tel que . Etablir l'injectivité de l'application
Correction
Soit et deux nombre réels. On a :
Or, deux nombres complexes sont égaux si et seulement s'ils ont la même partie réelle et même partie imaginaire. Donc, on a :
De fait, cela implique que :
Finalement :
Or, deux nombres complexes sont égaux si et seulement s'ils ont la même partie réelle et même partie imaginaire. Donc, on a :
De fait, cela implique que :
Finalement :
Question 2
Soit un intervalle inclus dans . On considère l'application suivante :
Déterminer le plus grand intervalle qui rend surjective.
Déterminer le plus grand intervalle qui rend surjective.
Correction
L'expression représente un polynôme de degré . En ce sens est continue. Comme le nombre présent devant le terme es , cela signifie que est convexe. De fait le graphe représentatif de présente un minimum en , tel que la dérivée première y soit nulle. Donc :
Le minimum vaut alors , avec :
Puis, on a :
Donc ceci nous permet d'affirmer que dans l'intervalle , chaque élément admet, au moins, un antécédent . En effet, on constate bien ceci graphiquement :
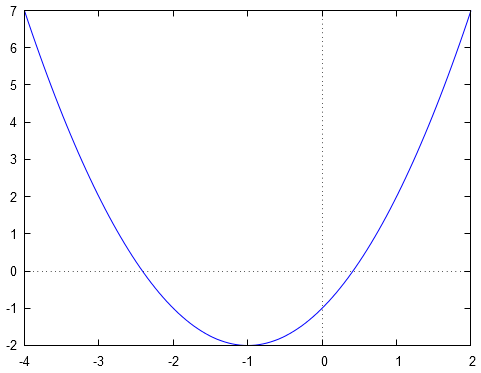 Ce qui nous permet de conclure que l'intervalle recherché est donné par :
Ce qui nous permet de conclure que l'intervalle recherché est donné par :
Le minimum vaut alors , avec :
Puis, on a :
Donc ceci nous permet d'affirmer que dans l'intervalle , chaque élément admet, au moins, un antécédent . En effet, on constate bien ceci graphiquement :

Question 3
Soit un nombre complexe. Démontrer que l'application est surjective.
Correction
Soit tel que .
Soit . Si on pose alors .
Ainsi, à chaque image il est toujours possible de trouver un antécédant car il suffit de choisir .
Finalement :
Soit . Si on pose alors .
Ainsi, à chaque image il est toujours possible de trouver un antécédant car il suffit de choisir .
Finalement :
Question 4
Démontrer que l'application est une bijection.
Correction
Nous allons vérifier l'assertion qui sert de définition à une bijection, à savoir :
Pour faire ceci, commençons par choisir un un réel quelconque . On a alors :
Donc, en multipliant par , on obtient :
Soit encore :
On a donc montrer que pour , on a :
On constate alors que :
si alors l'assertion de droite est fausse car ;
si alors l'assertion de droite est équivalente à .
Autrement dit, si l'image réelle alors il existe antécédent réel qui vaut .
Ainsi, on a bien démontré que :
Finalement :
On vérifie graphiquement ceci :
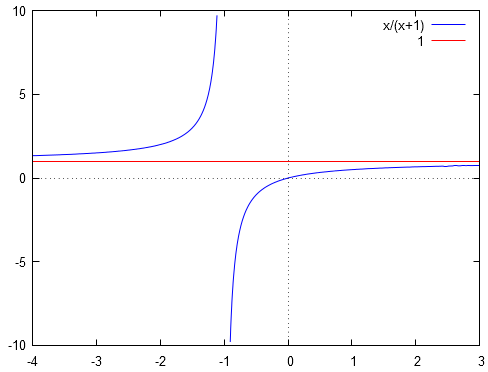
Pour faire ceci, commençons par choisir un un réel quelconque . On a alors :
Donc, en multipliant par , on obtient :
Soit encore :
On a donc montrer que pour , on a :
On constate alors que :
si alors l'assertion de droite est fausse car ;
si alors l'assertion de droite est équivalente à .
Autrement dit, si l'image réelle alors il existe antécédent réel qui vaut .
Ainsi, on a bien démontré que :
Finalement :
On vérifie graphiquement ceci :

Question 5
L'application est-elle une injection ? Justifier clairement.
Correction
Soit et deux nombre réels. On a :
On constate qu'il est possible d'avoir , c'est-à-dire que .
Finalement :
En effet, on vérifie facilement que . Il en résulte donc que n'est pas injective .
On constate qu'il est possible d'avoir , c'est-à-dire que .
Finalement :
En effet, on vérifie facilement que . Il en résulte donc que n'est pas injective .
Question 6
L'application est-elle une surjection ? Justifier clairement.
Correction
D'après la définition de l'application , on a . On constate que l'image n'admet pas d'antécédent par l'application .
En effet, graphiquement on vérifie ceci :
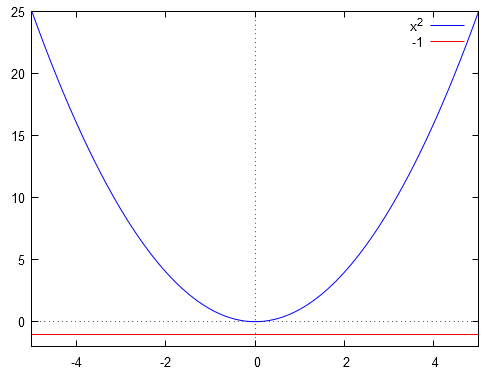 Finalement :
Finalement :
En effet, graphiquement on vérifie ceci :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.