Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
PROBLEME 2 - Exercice 1
50 min
70
Il s'agit de montrer que l'intégrale de GAUSS, notée , à pour valeur numérique :
C'est lui le génie !

Gauss était un génie particulièrement précoce : à 5 ans, le maître demandait de calculer 1+2+...+100, et Gauss inscrivit immédiatement le résultat sur son ardoise : ce n'est pas qu'il fut un génial calculateur, mais il avait trouvé une formule générale pour calculer de telles sommes.
A l'université, à 19 ans, il fut le premier à démontrer la loi de réciprocité quadratique, ce que ni Euler, ni Legendre n'avaient réussi. Au cours de sa vie, il en donnera huit preuves!!! Parmi ses autres prouesses, on peut citer la démonstration du théorème fondamental de l'algèbre, dans sa thèse de doctorat en 1799, l'invention de la théorie des congruences...
Le génie de Gauss se manifesta dans d'autres domaines : on lui doit d'importants travaux en électricité, en optique, en théorie du potentiel. Ainsi, le "gauss" est devenu l'unité d'induction magnétique.
Gauss acheva sa carrière de mathématicien en 1849, à l'occasion d'un jubilé en son honneur. Peu à peu, sa santé se détériore, et il meurt à Göttingen le 23 février 1855 pendant son sommeil.
Question 1
Quelle est la nature de l'intégrale ? Justifier.
Correction
L'intégrande est une application continue sur tout entier, donc de ce fait sur : l'ntégrande ne présente pas de singularité sur le domaine d'intégration. Ainsi l'intégrale n'est pas une intégrale impropre de deuxième espèce. En outre, la borne supérieure diverge vers , ce qui implique que l'intégrale de est une intégrale impropre de première espèce.
Question 2
Démontrer que l'intégrale est convergente.
Correction
On a :
Comme la fonction est continue sur alors elle est localement intégrable et de fait l'intégrale entre et existe bien.
On suppose maintenant que . On a alors :
Donc :
Comme la fonction exponentielle est strictement croissante sur alors elle y conserve l'ordre. De fait, on a :
Or, on sait que l'intégrale est de nature convergente. De fait, par application du théorème de comparaison, on peut affirmer que l'intégrale est elle même de nature convergente.
Or, on sait que :
En conclusion l'intégrale est convergente.
Comme la fonction est continue sur alors elle est localement intégrable et de fait l'intégrale entre et existe bien.
On suppose maintenant que . On a alors :
Donc :
Comme la fonction exponentielle est strictement croissante sur alors elle y conserve l'ordre. De fait, on a :
Or, on sait que l'intégrale est de nature convergente. De fait, par application du théorème de comparaison, on peut affirmer que l'intégrale est elle même de nature convergente.
Or, on sait que :
En conclusion l'intégrale est convergente.
Question 3
On pose :
Exprimer l'intégrale de en fonction de
Exprimer l'intégrale de en fonction de
Correction
On a :
Ainsi on a :
Ainsi on a :
Question 4
Exprimer l'intégrale en fonction de et de et .
Correction
L'intégrale s'écrit :
Soit :
Soit :
Question 5
En considérant la figure géométrique suivante :
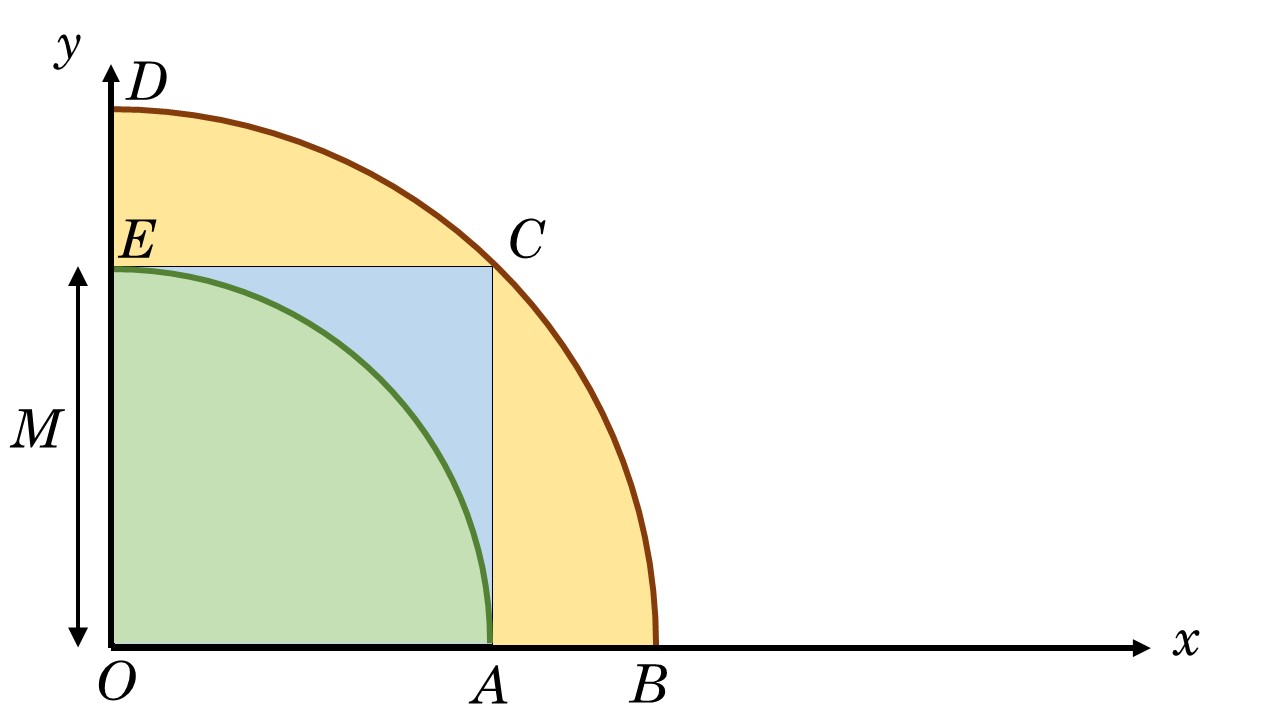
Sur cette figure, est un carré de côté et son domaine est noté . On note par le domaine circulaire et par le domaine circulaire . Justifier que l'on puisse écrire que :

Sur cette figure, est un carré de côté et son domaine est noté . On note par le domaine circulaire et par le domaine circulaire . Justifier que l'on puisse écrire que :
Correction
L'intégrale (double) est une intégrale de surface associée à l'intégrande toujours strictement positive. Donc cette intégrale représente le volume positif , présent sous la surface représentative de l'intégrande , et au dessus du domaine carré du plan de base.
Il est donc évident que plus la surface du domaine du plan sur lequel on détermine le volume est grand plus la valeur du volume (donc de l'intégrale associée) l'est également.
Or, d'après la figure proposée par le sujet, on constate immédiatement que :
Comme , cela implique immédiatement la double inégalité suivante :
Or, on peut écrire que :
et que
Donc, par interprétation géométrique de la double intégrale, on peut donc écrire :
Ceci est bien confirmée par la représentation graphique de l'intégrande qui permet de visualiser la proportionnalité du volume avec la surface du plan de base envisagée :
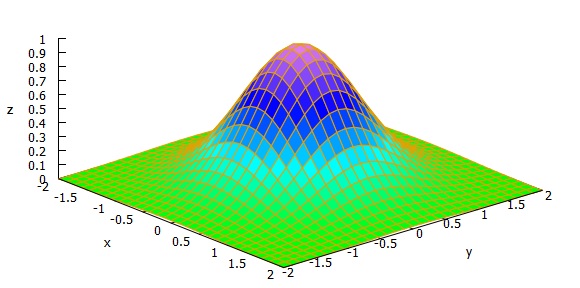
Il est donc évident que plus la surface du domaine du plan sur lequel on détermine le volume est grand plus la valeur du volume (donc de l'intégrale associée) l'est également.
Or, d'après la figure proposée par le sujet, on constate immédiatement que :
Comme , cela implique immédiatement la double inégalité suivante :
Or, on peut écrire que :
et que
Donc, par interprétation géométrique de la double intégrale, on peut donc écrire :
Ceci est bien confirmée par la représentation graphique de l'intégrande qui permet de visualiser la proportionnalité du volume avec la surface du plan de base envisagée :

Question 6
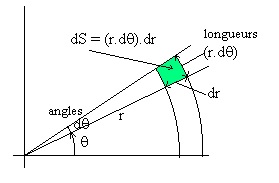
Comme les deux domaines d'intégration et sont \textit{circulaires} ont va donc introduire les coordonnées polaires et , bien mieux adaptées à cette configuration géométrique, afin de les paramétrer. On a alors l'élément de surface élémentaire du plan qui va s'écrire :
Justifier alors que la double inégalité précédente prenne maintenant la forme suivante :

Justifier alors que la double inégalité précédente prenne maintenant la forme suivante :
Correction
L'introduction des coordonnées polaires et va facilité le calcul des intégrales. En effet, comme le montre la du sujet, on a :
la grandeur va de l'origine à l'extrémité du domaine ou considéré. Ainsi pour , . Et pour , .
la variable angulaire démarre de (sur l'axe ) pour s'arrêter à (sur l'axe ) car les domaines et sont tous les deux des quarts de cercle.
Puis, Le sujet nous apprend que la quantité est un élément de surface du plan de base, et qui se transforme en coordonnées polaires par l'expression
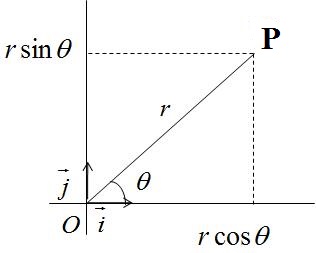
Enfin, notons par un point appartenant au domaine ou , et de coordonnées et définies par rapport à l'origine .
Par simple application du théorème de , on constate immédiatement que :
Ceci est bien montré sur la figure suivante :
D'où la transformation suivante de l'écriture de la double inégalité précédente :
la grandeur va de l'origine à l'extrémité du domaine ou considéré. Ainsi pour , . Et pour , .
la variable angulaire démarre de (sur l'axe ) pour s'arrêter à (sur l'axe ) car les domaines et sont tous les deux des quarts de cercle.
Puis, Le sujet nous apprend que la quantité est un élément de surface du plan de base, et qui se transforme en coordonnées polaires par l'expression
Enfin, notons par un point appartenant au domaine ou , et de coordonnées et définies par rapport à l'origine .
Par simple application du théorème de , on constate immédiatement que :
Ceci est bien montré sur la figure suivante :

D'où la transformation suivante de l'écriture de la double inégalité précédente :
Question 7
Démontrer que l'on a :
Correction
On constate que l'évolution angulaire est indépendante de l'évolution radiale (car l'intégrande ne dépend pas de ), donc de ce fait, il est possible de séparer explicitement les deux intégrales radiales et angulaires. Donc on a :
Avec , on trouve que :
Puis, on peut, par jeu d'écriture, écrire que :
Or, . Donc, on obtient :
Puis, inversons les bornes d'intégrations afin d'éliminer les signes . Dès lors, on trouve que :
L'intégration devient alors directe, et on obtient :
Avec , on trouve bien la double inégalité demandée, à savoir :
Avec , on trouve que :
Puis, on peut, par jeu d'écriture, écrire que :
Or, . Donc, on obtient :
Puis, inversons les bornes d'intégrations afin d'éliminer les signes . Dès lors, on trouve que :
L'intégration devient alors directe, et on obtient :
Avec , on trouve bien la double inégalité demandée, à savoir :
Question 8
En déduire, en justifiant clairement, la valeur de l'intégrale de .
Correction
Utilisons (parfois encore appelé théorème des gendarmes ou théorème du sandwich). On a alors :
Ce qui implique directement que
Soit :
Comme l'intégrande est positif, seule la possibilité positive est à retenir, et on a :
Finalement, on trouve que la valeur de l'intégrale de est :
Ce qui implique directement que
Soit :
Comme l'intégrande est positif, seule la possibilité positive est à retenir, et on a :
Finalement, on trouve que la valeur de l'intégrale de est :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.