Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
PROBLEME 1 - Exercice 1
45 min
65
Soit et deux réels, tel que . On cherche à déterminer la valeur de l'intégrale suivante :
On considère la figure géométrique suivante :
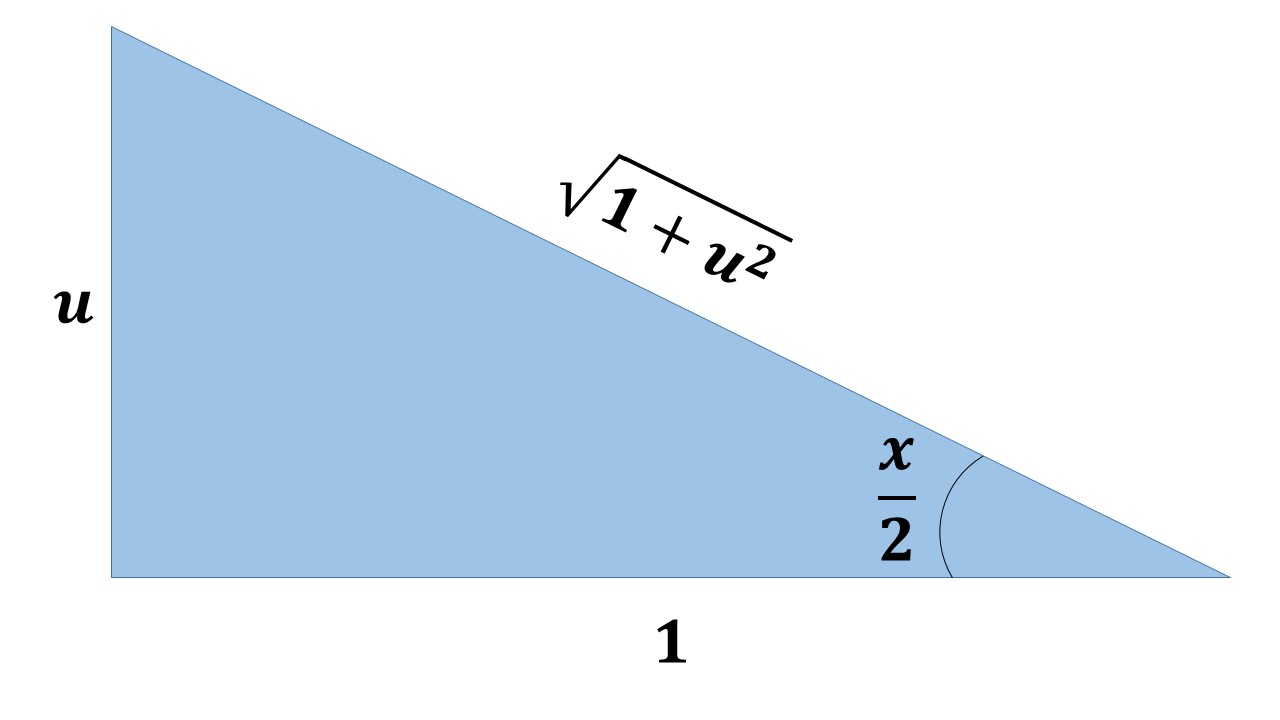
On considère la figure géométrique suivante :

Question 1
Quelle est la nature de l'intégrale ? Justifier.
Correction
L'intégrale n'est pas une intégrale généralisée (on dit également impropre) de première espèce puisqu'aucune de ses bornes n'est infinie.
Étudions maintenant l'éventuelle présence d'une singularité appartenant au domaine d'intégration. On a alors :
Or, par hypothèse, on sait que , d'où :
Or , il est impossible d'avoir . Ainsi, il est donc impossible d'avoir la condition . Autrement dit, on a :
Ainsi, l'intégrande existe sur l'intervalle d'intégration , et donc l'intégrale n'est pas une intégrale impropre de deuxième espèce et donc nécessairement pas de troisième espèce.
De plus, la fonction est dérivable sur , car :
Ainsi, l'intégrande est dérivable sur et donc y est continue. Donc n'est pas une intégrale propre.
Étudions maintenant l'éventuelle présence d'une singularité appartenant au domaine d'intégration. On a alors :
Or, par hypothèse, on sait que , d'où :
Or , il est impossible d'avoir . Ainsi, il est donc impossible d'avoir la condition . Autrement dit, on a :
Ainsi, l'intégrande existe sur l'intervalle d'intégration , et donc l'intégrale n'est pas une intégrale impropre de deuxième espèce et donc nécessairement pas de troisième espèce.
De plus, la fonction est dérivable sur , car :
Ainsi, l'intégrande est dérivable sur et donc y est continue. Donc n'est pas une intégrale propre.
Question 2
Effectuer le changement de variable , et en vous aidant de la figure géométrique associée au changement de variable, démontrer que : .
Correction
Effectuons le changement de variable , et à l'aide de la figure géométrique on a :
Donc, on peut écrire que :
Finalement :
Donc, on peut écrire que :
Finalement :
Question 3
Démontrer que ce changement de variable permet d'écrire que :
Correction
On a :
Donc en dérivant, on obtient :
D'où :
Donc en dérivant, on obtient :
D'où :
Question 4
Quelles sont les bornes de l'intégrale en ?
Correction
Les bornes de l'intégrale en sont :
Si alors ;
Si alors ;
Si alors ;
Si alors ;
Question 5
Démontrer que :
Correction
On a :
Soit :
Ce qui nous donne encore :
Donc, en factorisant par , on trouve que :
Finalement, on trouve bien que :
Soit :
Ce qui nous donne encore :
Donc, en factorisant par , on trouve que :
Finalement, on trouve bien que :
Question 6
Effectuer maintenant le changement de variable , démontrer que :
avec :
avec :
Correction
Effectuons le changement de variable suivant :
Ainsi :
Donc on obtient :
Ce qui donne :
Soit encore :
En simplifiant on obtient :
Que l'on écrit encore :
En utilisant une identité remarquable, on trouve bien :
avec :
Ainsi :
Donc on obtient :
Ce qui donne :
Soit encore :
En simplifiant on obtient :
Que l'on écrit encore :
En utilisant une identité remarquable, on trouve bien :
avec :
Question 7
Quelle est l'espèce de l'intégrale ? Justifier.
Correction
L'intégrale est de première espèce car sa borne supérieure est infinie.
Question 8
Calculer la valeur de l'intégrale généralisé (on dit parfois impropre) .
Correction
On a :
Donc, on obtient :
Donc, on obtient :
Question 9
En déduire la valeur de .
Correction
Donc la valeur de est :
En simplifiant :
En simplifiant :
Question 10
Donner la valeur exacte de .
Correction
La valeur exacte de est :
Finalement :
Finalement :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.