Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Tchat avec un prof
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercice 10 - Exercice 1
1 h
90
Pour réaliser cet exercice plus délicat, il est préférable d'avoir réalisé le précédent.
Question 1
Démontrer que l'intégrale, dite de , est convergente
Correction
L'intégrale de va être écrite suivant la décomposition suivante :
Or, on sait que :
et que la fonction est, en la prolongeant par continuité par la valeur image à l'origine, continue donc localement intégrable.
Donc l'intégrale converge. Puis, on a :
Soit :
D'où :
Donc :
Or, on a :
Mais :
Ainsi, on peut écrire que :
Or, lors de l'exercice précédent nous avons démontré que, l'intégrale converge. Ainsi, l'intégrale de est convergente.
Or, on sait que :
et que la fonction est, en la prolongeant par continuité par la valeur image à l'origine, continue donc localement intégrable.
Donc l'intégrale converge. Puis, on a :
Soit :
D'où :
Donc :
Or, on a :
Mais :
Ainsi, on peut écrire que :
Or, lors de l'exercice précédent nous avons démontré que, l'intégrale converge. Ainsi, l'intégrale de est convergente.
Question 2
Démontrer que l'intégrale, dite de , est semi-convergente.
Conseil : vous pourrez écrire, en justifiant, que :
puis, sur chaque intervalles , minorer par . Pensez à faire des schémas sur pour vous en convaincre.
Conseil : vous pourrez écrire, en justifiant, que :
puis, sur chaque intervalles , minorer par . Pensez à faire des schémas sur pour vous en convaincre.
Correction
Démontrons maintenant que l'intégrale de est semi-convergente.
Pour strictement positif, on peut écrire que :
En utilisant la relation de Chasles intégrale, on obtient :
Soit sous forme plus compacte :
Or, sur chaque sur chaque intervalles , on a la relation de minoration du terme suivante :
Ceci va nous permettre d'envisager l'emploi d'un critère de comparaison. En effet illustrons cette inégalité graphiquement.
On a par exemple, pour donc sur l'intervalle , la minoration de par (voir le figure ci après) :
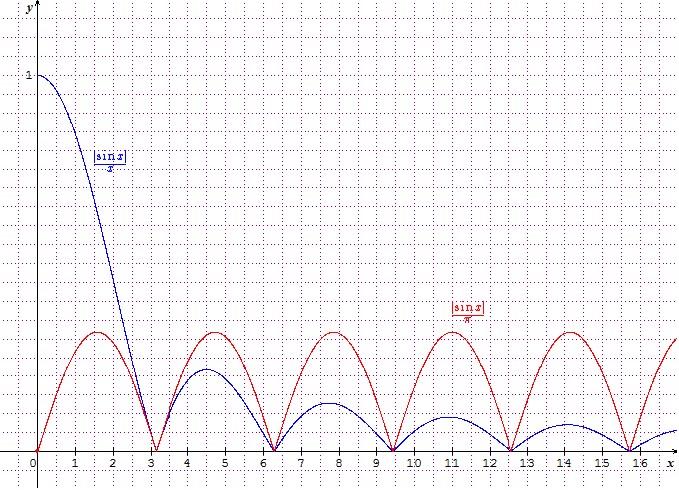
Et de même pour , donc sur l'intervalle , on a la minoration de par :
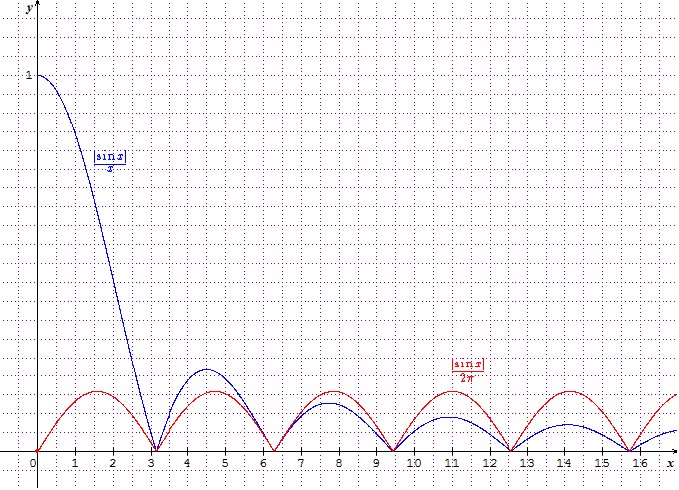
Dès lors, par intégration sur , on peut écrire que :
Soit encore :
Or, avec la présence de la valeur absolue :
Donc, on obtient :
Ce qui nous conduit à pouvoir écrire la sommation suivante :
En remarquant que
on trouve que :
Passons maintenant à la limite lorsque , on trouve alors :
Il suffit alors de remarquer que la somme minorante qui apparaît est la qui .
Donc, en vertu du critère de comparaison, le terme diverge lui aussi de ce fait.
Or, ce terme divergent n'est autre que l'intégrale .
Ainsi, sur .
Nous venons de démontrer que l'intégrale de converge, mais que l'intégrale diverge. Finalement l'intégrale de est semi-convergente.
Pour strictement positif, on peut écrire que :
En utilisant la relation de Chasles intégrale, on obtient :
Soit sous forme plus compacte :
Or, sur chaque sur chaque intervalles , on a la relation de minoration du terme suivante :
Ceci va nous permettre d'envisager l'emploi d'un critère de comparaison. En effet illustrons cette inégalité graphiquement.
On a par exemple, pour donc sur l'intervalle , la minoration de par (voir le figure ci après) :

Et de même pour , donc sur l'intervalle , on a la minoration de par :

Dès lors, par intégration sur , on peut écrire que :
Soit encore :
Or, avec la présence de la valeur absolue :
Donc, on obtient :
Ce qui nous conduit à pouvoir écrire la sommation suivante :
En remarquant que
on trouve que :
Passons maintenant à la limite lorsque , on trouve alors :
Il suffit alors de remarquer que la somme minorante qui apparaît est la qui .
Donc, en vertu du critère de comparaison, le terme diverge lui aussi de ce fait.
Or, ce terme divergent n'est autre que l'intégrale .
Ainsi, sur .
Nous venons de démontrer que l'intégrale de converge, mais que l'intégrale diverge. Finalement l'intégrale de est semi-convergente.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.