Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Une équation différentielle classique en Mécanique - Exercice 1

45 min
70
Il existe des équations différentielles "modèles" qui interviennent dans de très nombreux domaines. Cela signifie qu'il existe des comportements similaires dans de nombreux domaines des Sciences. En voici un exemple.
Question 1
On note par tt le temps, qui est le paramètre d'évolution en Physique classique. On a alors t⩾0t \geqslant 0.
On considère l'équation différentielle suivante, qui modélise le comportement oscillatoire d'une quantité ff qui caractérise un système physique réel :
d2 fdt2(t)+2λd fdt(t)+ω02 f(t)=Acos⁡(ωt)\dfrac{d^2\, f}{dt^2}(t) + 2\lambda \dfrac{d\, f}{dt}(t) + \omega_0^2 \, f(t) = A \cos(\omega t)
Dans cette équation différentielle linéaire, du second ordre, à coefficients constants, on a :
∙  {\color{blue}{\bullet \,\,}} le terme λ\lambda caractérise l'amortissement temporel de ff, et est un réel strictement positif ;
∙  {\color{blue}{\bullet \,\,}} le terme ω0\omega_0 caractérise l'oscillation intrinsèque (on dit aussi propre) de ff, et est un réel strictement positif ;
∙  {\color{blue}{\bullet \,\,}} le terme AA caractérise l'amplitude de l'excitation externe du système physique, et est un réel strictement positif ;
∙  {\color{blue}{\bullet \,\,}} le terme ω\omega caractérise l'oscillation externe du système (on dit aussi que c'est celle d'un opérateur extérieur), et est également un réel strictement positif.
Pour des raisons purement d'ordre physique, on admettra que la  condition  suivante  est  toujours  reˊaliseˊe{\color{red}{la \,\, condition \,\, suivante \,\, est \,\, toujours \,\, réalisée}} lors de cet exercice : λ<ω0{\color{red}{\lambda < \omega_0}}
Les deux {\color{blue}{\textbf{conditions initiales}}}, qui définissent le problème de \textit{Cauchy} considéré, sont les suivantes :
{f(t=0)=0d fdt(t=0)=0{\color{blue}{\left\lbrace \begin{array}{rcl} f(t=0) & = & 0 \\ & & \\ \dfrac{d \, f}{dt}(t=0) & = & 0 \\ \end{array} \right.}}
On adoptera la notation simplificatrice suivante :
Ω=ω02−λ2>0\Omega = \sqrt{\omega_0^2 - \lambda^2} > 0

Déterminer le discriminant Δ\Delta associée à l'équation caractéristique de l'équation différentielle, et précisez son signe.

Correction
Le discriminant Δ\Delta, associée à l'équation caractéristique de l'équation différentielle, est :
Δ=(2λ)2−4×1×ω02=4λ2−4ω02=4(λ2−ω02)\Delta = (2\lambda)^2 -4 \times 1 \times \omega_0^2 = 4\lambda^2 - 4\omega_0^2 = 4(\lambda^2 - \omega_0^2)
Soit encore, avec l'hypothèse 0<λ<ω00 < \lambda < \omega_0, l'expression suivante :
Δ=4(λ2−ω02)<0{\color{red}{\boxed{\Delta = 4(\lambda^2 - \omega_0^2) < 0}}}
Question 2

En déduire les expressions des racines de cette équation caractéristique.

Correction
Les expressions des deux racines r1r_1 et r2r_2, complexes conjuguées l'une de l'autre, de cette équation caractéristique sont (avec i2=−1i^2 = -1) :
{r1=−2λ+i−4(λ2−ω02)2r2=−2λ−i−4(λ2−ω02)2\left\lbrace\begin{array}{rcl} r_1 & = & \dfrac{-2\lambda + i \sqrt{-4(\lambda^2 - \omega_0^2)}}{2} \\ & & \\ r_2 & = & \dfrac{-2\lambda - i \sqrt{-4(\lambda^2 - \omega_0^2)}}{2} \\ \end{array}\right.
En simplifiant :
{r1=−λ+iω02−λ2r2=−λ−iω02−λ2\left\lbrace \begin{array}{rcl} r_1 & = & -\lambda + i \sqrt{ \omega_0^2 - \lambda^2} \\ & & \\ r_2 & = & -\lambda - i \sqrt{ \omega_0^2 - \lambda^2} \\ \end{array} \right.
Soit :
{r1=−λ+i Ωr2=−λ−i Ω{\color{red}{\boxed{ \left\lbrace \begin{array}{rcl} r_1 & = & -\lambda + i \, \Omega \\ & & \\ r_2 & = & -\lambda - i \, \Omega \\ \end{array} \right.}}}
Question 3

En déduire l'expression de la solution homogène, notée fH(t)f_H(t), de l'équation différentielle proposée.

Correction
L'expression de la solution homogène, notée fH(t)f_H(t), de l'équation différentielle proposée est :
fH(t)=e−λt(Acos⁡(Ωt)+Bsin⁡(Ωt))    avec :  (A ; B)∈R2 {\color{red}{\boxed{ f_H(t) = e^{-\lambda t} \left( \mathcal{A} \cos(\Omega t) + \mathcal{B} \sin (\Omega t)\right) \,\,\,\, \mathrm{avec}\, : \,\, (\mathcal{A}\,;\,\mathcal{B}) \in \mathbb{R}^2 }}}
Question 4

La solution particulière recherchée, notée fP(t)f_P(t), de l'équation différentielle proposée, sera choisie de la forme suivante :
fP(t)=αcos⁡(ωt)+βsin⁡(ωt)f_P(t) = \alpha \cos(\omega t) + \beta \sin(\omega t)
Avec α\alpha et β\beta qui sont deux nombres réels.
Déterminer l'expression de fP(t)f_P(t) associée à notre problème, c'est-à-dire les expressions des deux coefficients réels α\alpha et β\beta.

Correction
La solution particulière recherchée, notée fP(t)f_P(t), de l'équation différentielle proposée, sera choisie de la forme suivante :
fP(t)=αcos⁡(ωt)+βsin⁡(ωt)f_P(t) = \alpha \cos(\omega t) + \beta \sin(\omega t)
Avec α\alpha et β\beta qui sont deux nombres réels. Ainsi :
d fPdt(t)=fP′(t)=−αωsin⁡(ωt)+βωcos⁡(ωt)\dfrac{d \, f_P}{dt}(t) = f'_P(t) = - \alpha \omega \sin(\omega t) + \beta \omega \cos(\omega t)
Et aussi :
d2 fPdt2(t)=fP′′(t)=(fP′(t))′=−αω2cos⁡(ωt)−βω2sin⁡(ωt)\dfrac{d^2 \, f_P}{dt^2}(t) = f''_P(t) = \left( f'_P(t) \right)' = - \alpha \omega^2 \cos(\omega t) - \beta \omega^2 \sin(\omega t)
Donc, en remplaçant dans l'équation différentielle originelle, on obtient :
−αω2cos⁡(ωt)−βω2sin⁡(ωt)+2λ(−αωsin⁡(ωt)+βωcos⁡(ωt))+ω02(αcos⁡(ωt)+βsin⁡(ωt))=Acos⁡(ωt)\begin{array}{l} - \alpha \omega^2 \cos(\omega t) - \beta \omega^2 \sin(\omega t) + 2\lambda \left( - \alpha \omega \sin(\omega t) + \beta \omega \cos(\omega t) \right) + \omega_0^2 \left( \alpha \cos(\omega t) + \beta \sin(\omega t) \right) \\ = A \cos(\omega t) \end{array}
Soit encore :
(−αω2+2λβω+αω02)cos⁡(ωt)+(−βω2−2λαω+βω02)sin⁡(ωt)=Acos⁡(ωt)+0sin⁡(ωt)\left( - \alpha \omega^2 + 2\lambda \beta \omega + \alpha \omega_0^2 \right) \cos(\omega t) + \left( - \beta \omega^2 - 2\lambda \alpha \omega + \beta \omega_0^2 \right) \sin(\omega t) = A \cos(\omega t) + 0 \sin(\omega t)
D'où :
(α(ω02−ω2)+2λβω)cos⁡(ωt)+(β(ω02−ω2)−2λαω)sin⁡(ωt)=<br/>Acos⁡(ωt)+0sin⁡(ωt)\left( {\color{red}{\alpha (\omega_0^2 - \omega^2) + 2\lambda \beta \omega}} \right) \cos(\omega t) + \left( {\color{blue}{\beta (\omega_0^2 - \omega^2) - 2\lambda \alpha \omega}} \right) \sin(\omega t) = <br /> {\color{red}{A}} \cos(\omega t) + {\color{blue}{0}} \sin(\omega t)
On obtient alors le système suivant :
{α(ω02−ω2)+2λβω=Aβ(ω02−ω2)−2λαω=0\left\lbrace \begin{array}{rcl} {\color{red}{\alpha (\omega_0^2 - \omega^2) + 2\lambda \beta \omega}} & = & {\color{red}{A}} \\ & & \\ {\color{blue}{\beta (\omega_0^2 - \omega^2) - 2\lambda \alpha \omega}} & = & {\color{blue}{0}} \\ \end{array} \right.
Ainsi, on en déduit que :
α=(ω02−ω2)β2λω{\color{blue}{\alpha}} = {\color{blue}{\dfrac{(\omega_0^2 - \omega^2) \beta}{2\lambda \omega}}}
On a alors :
(ω02−ω2)β2λω(ω02−ω2)+2λβω=A{\color{blue}{\dfrac{(\omega_0^2 - \omega^2) \beta}{2\lambda \omega}}} {\color{red}{(\omega_0^2 - \omega^2) + 2\lambda \beta \omega}} = {\color{red}{A}}
Soit encore :
β((ω02−ω2)22λω+2λω)=A\beta \left( \dfrac{(\omega_0^2 - \omega^2)^2 }{2\lambda \omega} + 2\lambda \omega \right) = A
Ce qui nous donne :
β((ω02−ω2)2+4λ2ω22λω)=A\beta \left( \dfrac{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2}{2\lambda \omega} \right) = A
Ainsi :
β=2λωA(ω02−ω2)2+4λ2ω2\beta = \dfrac{2\lambda \omega A}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2}
On en déduit alors que :
α=(ω02−ω2)2λω2λωA(ω02−ω2)2+4λ2ω2{\color{blue}{\alpha}} = {\color{blue}{\dfrac{(\omega_0^2 - \omega^2)}{2\lambda \omega}}} \dfrac{2\lambda \omega A}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2}
En simplifiant:
α=(ω02−ω2)A(ω02−ω2)2+4λ2ω2\alpha = \dfrac{(\omega_0^2 - \omega^2) A}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2}
Dès lors, l'expression de fP(t)f_P(t) devient :
fP(t)=(ω02−ω2)A(ω02−ω2)2+4λ2ω2cos⁡(ωt)+2λωA(ω02−ω2)2+4λ2ω2sin⁡(ωt)f_P(t) = \dfrac{(\omega_0^2 - \omega^2) A}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} \cos(\omega t) + \dfrac{2\lambda \omega A}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} \sin(\omega t)
En factorisant :
fP(t)=A(ω02−ω2)2+4λ2ω2((ω02−ω2)cos⁡(ωt)+2λωsin⁡(ωt)){\color{red}{\boxed{f_P(t) = \dfrac{A}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} \left( (\omega_0^2 - \omega^2) \cos(\omega t) + 2\lambda \omega \sin(\omega t)\right)}}}
Question 5

Donner alors l'expression de la solution mathématique globale f(t)f(t) ainsi recherchée.

Correction
L'expression de la solution mathématique globale f(t)f(t) est donc donnée par :
f(t)=fH(t)+fP(t)f(t) = f_H(t) + f_P(t)
A savoir, avec (A ; B)∈R2(\mathcal{A}\,;\,\mathcal{B}) \in \mathbb{R}^2 :
f(t)=e−λt(Acos⁡(Ωt)+Bsin⁡(Ωt))+A(ω02−ω2)2+4λ2ω2((ω02−ω2)cos⁡(ωt)+2λωsin⁡(ωt)){\color{red}{\boxed{ f(t) = e^{-\lambda t} \left( \mathcal{A} \cos(\Omega t) + \mathcal{B} \sin (\Omega t)\right) + \dfrac{A}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} \left( (\omega_0^2 - \omega^2) \cos(\omega t) + 2\lambda \omega \sin(\omega t)\right)}}}
Question 6

A l'aide des deux conditions  initiales{\color{blue}{conditions \,\, initiales}} proposées, déterminer l'expression de la solution physique f(t)f(t) qui décrit le comportement oscillant réel de ff.

Correction
Les deux conditions initiales proposées sont :
{f(t=0)=0d fdt(t=0)=0\left\lbrace \begin{array}{rcl} f(t=0) & = & 0 \\ & & \\ \dfrac{d \, f}{dt}(t=0) & = & 0 \\ \end{array} \right.
Or, on a :
f(t=0)=e−λ0(Acos⁡(Ω0)+Bsin⁡(Ω0))+A(ω02−ω2)2+4λ2ω2((ω02−ω2)cos⁡(ω0)+2λωsin⁡(ω0))f(t=0) = e^{-\lambda 0} \left( \mathcal{A} \cos(\Omega 0) + \mathcal{B} \sin (\Omega 0)\right) + \dfrac{A}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} \left( (\omega_0^2 - \omega^2) \cos(\omega 0) + 2\lambda \omega \sin(\omega 0)\right)
Soit encore :
f(t=0)=A+A(ω02−ω2)2+4λ2ω2(ω02−ω2)f(t=0) = \mathcal{A} + \dfrac{A}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} (\omega_0^2 - \omega^2)
La première des deux conditions initiales nous donne :
A+A(ω02−ω2)(ω02−ω2)2+4λ2ω2=0\mathcal{A} + \dfrac{A(\omega_0^2 - \omega^2)}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} = 0
Ce qui nous conduit à l'expression de A\mathcal{A} :
A=−A(ω02−ω2)(ω02−ω2)2+4λ2ω2\mathcal{A} = - \dfrac{A(\omega_0^2 - \omega^2)}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2}
Maintenant, déterminons l'expression de la dérivée première temporelle f′f'. On a alors :
f′(t)=−λe−λt(Acos⁡(Ωt)+Bsin⁡(Ωt))+Ω e−λt(−Asin⁡(Ωt)+Bcos⁡(Ωt))+Aω(ω02−ω2)2+4λ2ω2(−(ω02−ω2)sin⁡(ωt)+2λωcos⁡(ωt))\begin{array}{rcl} f'(t) & = & -\lambda e^{-\lambda t} \left( \mathcal{A} \cos(\Omega t) + \mathcal{B} \sin (\Omega t)\right) + \Omega \, e^{-\lambda t} \left( - \mathcal{A} \sin(\Omega t) + \mathcal{B} \cos (\Omega t)\right) \\ & + & \dfrac{A\omega}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} \left( - (\omega_0^2 - \omega^2) \sin(\omega t) + 2\lambda \omega \cos(\omega t)\right) \end{array}
Posons maintenant t=0t=0, on obtient alors :
f′(t=0)=−λe−λ0(Acos⁡(Ω0)+Bsin⁡(Ω0))+Ω e−λ0(−Asin⁡(Ω0)+Bcos⁡(Ω0))+Aω(ω02−ω2)2+4λ2ω2(−(ω02−ω2)sin⁡(ω0)+2λωcos⁡(ω0))\begin{array}{rcl} f'(t=0) & = & -\lambda e^{-\lambda 0} \left( \mathcal{A} \cos(\Omega 0) + \mathcal{B} \sin (\Omega 0)\right) + \Omega \, e^{-\lambda 0} \left( - \mathcal{A} \sin(\Omega 0) + \mathcal{B} \cos (\Omega 0)\right) \\ & + & \dfrac{A\omega}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} \left( - (\omega_0^2 - \omega^2) \sin(\omega 0) + 2\lambda \omega \cos(\omega 0)\right) \end{array}
Soit encore :
f′(t=0)=−λA+ΩB+Aω(ω02−ω2)2+4λ2ω2(2λω)f'(t=0) = -\lambda \mathcal{A} + \Omega \mathcal{B} + \dfrac{A\omega}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} \left( 2\lambda \omega \right)
Mais également :
f′(t=0)=−λA+ΩB+2λω2A(ω02−ω2)2+4λ2ω2f'(t=0) = -\lambda \mathcal{A} + \Omega \mathcal{B} + \dfrac{ 2\lambda\omega^2 A}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2}
Ainsi, la seconde condition initiale nous donne :
−λA+ΩB+2λω2A(ω02−ω2)2+4λ2ω2=0-\lambda \mathcal{A} + \Omega \mathcal{B} + \dfrac{ 2\lambda\omega^2 A}{(\omega_0^2 - \omega^2)^2 +4\lambda^2 \omega^2} = 0
Ce qui nous permet d'écrire que :
ΩB=λA−2λω2A(ω02−ω2)2+4λ2ω2\Omega \mathcal{B} = \lambda \mathcal{A} - \dfrac{ 2\lambda\omega^2 A}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2}
Soit :
ΩB=−Aλ(ω02−ω2)(ω02−ω2)2+4λ2ω2−2λω2A(ω02−ω2)2+4λ2ω2\Omega \mathcal{B} = - \dfrac{A\lambda(\omega_0^2 - \omega^2)}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} - \dfrac{ 2\lambda\omega^2 A}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2}
Donc :
ΩB=−Aλ(ω02−ω2)2+4λ2ω2((ω02−ω2)+2ω2)\Omega \mathcal{B} = - \dfrac{A\lambda}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} \left( (\omega_0^2 - \omega^2) + 2\omega^2 \right)
Ce qui nous donne :
ΩB=−Aλ(ω02−ω2)2+4λ2ω2(ω02−ω2+2ω2)\Omega \mathcal{B} = - \dfrac{A\lambda}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} \left( \omega_0^2 - \omega^2 + 2\omega^2 \right)
On aboutit alors à :
ΩB=−Aλ(ω02−ω2)2+4λ2ω2(ω02+ω2)\Omega \mathcal{B} = - \dfrac{A\lambda}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} \left( \omega_0^2 + \omega^2 \right)
Finalement :
B=−Aλ(ω02+ω2)Ω((ω02−ω2)2+4λ2ω2)\mathcal{B} = - \dfrac{A\lambda (\omega_0^2 + \omega^2)}{\Omega\left((\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2 \right)}
Donc, la solution f(t)f(t) qui satisfait à notre problème de CauchyCauchy est donc donnée par :
f(t)=e−λt(−A(ω02−ω2)(ω02−ω2)2+4λ2ω2cos⁡(Ωt)−Aλ(ω02+ω2)Ω((ω02−ω2)2+4λ2ω2)sin⁡(Ωt))+A(ω02−ω2)2+4λ2ω2((ω02−ω2)cos⁡(ωt)<br/>+2λωsin⁡(ωt))\begin{array}{rcl} f(t) & = & e^{-\lambda t} \left( - \dfrac{A(\omega_0^2 - \omega^2)}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} \cos(\Omega t) - \dfrac{A\lambda (\omega_0^2 + \omega^2)}{\Omega\left((\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2 \right)} \sin (\Omega t)\right) \\ & & \\ & + & \dfrac{A}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} \left( (\omega_0^2 - \omega^2) \cos(\omega t) <br />+ 2\lambda \omega \sin(\omega t)\right) \\ \end{array}
En factorisant, on obtient :
f(t)=−A(ω02−ω2)2+4λ2ω2e−λt((ω02−ω2)cos⁡(Ωt)−λ(ω02+ω2)Ωsin⁡(Ωt))+A(ω02−ω2)2+4λ2ω2((ω02−ω2)cos⁡(ωt)<br/>+2λωsin⁡(ωt))\begin{array}{rcl} f(t) & = & - \dfrac{A}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} e^{-\lambda t} \left((\omega_0^2 - \omega^2) \cos(\Omega t) - \dfrac{\lambda (\omega_0^2 + \omega^2)}{\Omega} \sin (\Omega t)\right) \\ & & \\ & + & \dfrac{A}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} \left( (\omega_0^2 - \omega^2) \cos(\omega t) <br />+ 2\lambda \omega \sin(\omega t)\right) \\ \end{array}
Finalement, on trouve que :
f(t)=A(ω02−ω2)2+4λ2ω2(−e−λt(<br/>(ω02−ω2)cos⁡(Ωt)−λ(ω02+ω2)Ωsin⁡(Ωt))+(ω02−ω2)cos⁡(ωt)+2λωsin⁡(ωt)){\color{red}{\boxed{ \begin{array}{rcl} f(t) & = & \dfrac{A}{(\omega_0^2 - \omega^2)^2 + 4\lambda^2 \omega^2} \left( - e^{-\lambda t} \left( <br />(\omega_0^2 - \omega^2) \cos(\Omega t) - \dfrac{\lambda (\omega_0^2 + \omega^2)}{\Omega} \sin (\Omega t)\right) \right. \\ & & \\ & + & (\omega_0^2 - \omega^2) \cos(\omega t) + 2\lambda \omega \sin(\omega t) \Big) \\ \end{array}}}}
Question 7

On note par TT une quantité qui à les dimension d'un temps, et qui caractérise le comportement oscillatoire de ff. Cette quantité TT s'appelle la " pseudo-peˊriode{\color{red}{\textbf{pseudo-période}}} de ff. Est-il possible, et pourquoi, de définir TT par la relation T=2πΩT = \dfrac{2\pi}{\Omega} ?

Correction
Il est impossible{\color{red}{\boxed{{\color{red}{\textbf{impossible}}}}}} de définir TT par la relation T=2πΩT = \dfrac{2\pi}{\Omega} car la solution trouvée précédemment présente des termes trigonométriques d'arc Ωt\Omega t mais aussi d'arc ωt\omega t. Ces deux arcs sont, à priori, différents, d'où l'impossibilité de la formule proposée pour TT.
Question 8

Parmi les trois courbes proposées sur le graphique ci-dessous, pour t∈[0 ; 8]t \in [0\,;\,8], laquelle est selon vous celle qui correspond à un comportement physique qui peut être modélisé par les conditions de notre exercice ? Indiquer clairement sa couleur : rouge{\color{red}{\textbf{rouge}}}, bleue{\color{blue}{\textbf{bleue}}} ou vert{\color{green}{\textbf{vert}}}. Bien évidemment, votre choix sera accompagné d'une justification\textbf{justification} claire, argumentée, et sans ambiguïté.

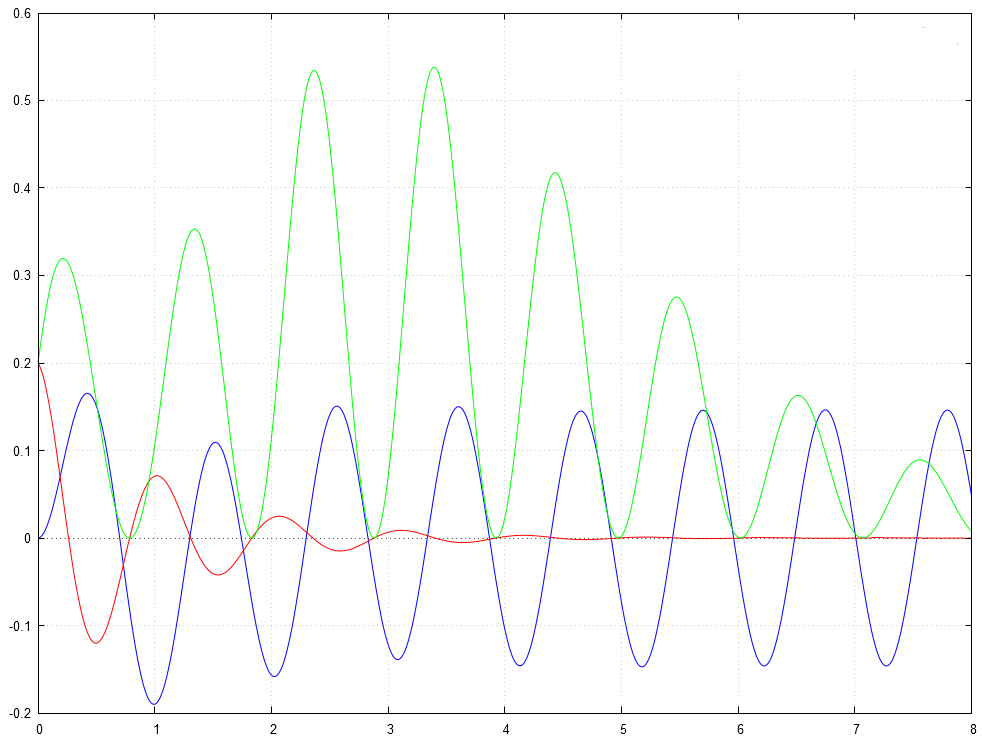
Correction
Seule la solution graphique de couleur bleue bleue{\color{blue}{\textbf{bleue}}} satisfait aux deux conditions initiales.
Donc la bonne solution est la courbe de couleur bleue{\color{red}{\boxed{{\color{blue}{\textbf{bleue}}}}}}.