Qui aura 20 en maths ?

💯 Le grand concours 100% Terminale revient le 31 mai 2026 en ligne !Découvrir  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Un bon café - Exercice 1

20 min
35
Un exemple de problème de thermique qui se modélise par une EDO du premier ordre.
Question 1
On note par TT la température, et par tt le temps. On convient qu'une unité de temps correspond à une minute et la température est mesuré en degré Celsius.
Considérons une tasse de café à la température de 75 ∘C75\,^\circ C dans une salle à 25 ∘C25\,^\circ C. Après cinq minutes le café est à 50 ∘C50\,^\circ C. Si on suppose que la vitesse de refroidissement du café est proportionnelle à la différence des températures, c'est-à-dire que la température du café suit la loi de Newton{\color{blue}{\textit{la loi de Newton}}}, cela signifie qu'il existe une constante K<0K < 0 telle que la température vérifie l’EDO du premier ordre
d Tdt(t)=K(T(t)−25)\dfrac{d \, T}{dt}(t) = K \left( T(t) - 25 \right)
La condition physique associée est :
T(t=5)=50 ∘CT(t=5) = 50\,^\circ C

Déterminer formellement l'équation différentielle vérifiée par la fonction température TT.

Correction
On a :
d Tdt(t)=KT(t)−25K\dfrac{d \, T}{dt}(t) = K T(t) - 25 K
Soit :
d Tdt(t)−KT(t)=−25K{\color{red}{\boxed{\dfrac{d \, T}{dt}(t) - K T(t) = - 25 K }}}
Question 2

Déterminer la solution homogène THT_H.

Correction
La solution homogène THT_H est donnée par :
d THdt(t)−KTH(t)=0    ⟹    TH(t)=A e−−K1t\dfrac{d \, T_H}{dt}(t) - K T_H(t) = 0 \,\,\,\, \Longrightarrow \,\,\,\, T_H(t) = A \, e^{-\frac{-K}{1}t}
Soit :
TH(t)=A eKt{\color{red}{\boxed{T_H(t) = A \, e^{Kt} }}}
Question 3

Déterminer la solution particulière TPT_P.

Correction
Comme le second membre est −25K∈R- 25 K \in \mathbb{R} alors le second membre est de même nature, à savoir :
TP(t)=D∈R{\color{red}{\boxed{T_P(t) = D \in \mathbb{R} }}}
Question 4

Déterminer la forme de la solution mathématique TT.

Correction
La solution mathématique TT est donnée par :
T(t)=TH(t)+TP(t)=A eKt+D   (A ; D)∈R2{\color{red}{\boxed{T(t) = T_H(t) + T_P(t) = A \, e^{Kt} + D \,\,\, (A\,;\,D) \in \mathbb{R}^2 }}}
Question 5

Déterminer la solution qui satisfait à la condition physique imposée.

Correction
On sait qu'au départ, à t=0t=0, la température du café est de 75 ∘C75\,^\circ C. Donc :
75=A eK0+D    ⟺    75=A+D75 = A \, e^{K0} + D \,\,\,\, \Longleftrightarrow \,\,\,\, 75 = A+D
Puis, on sait qu'au bout d'un temps \og infiniment \fg long la température du café sera de 25 ∘C25\,^\circ C. Donc :
lim⁡t⟶+∞T(t)=25    ⟺    lim⁡t⟶+∞(A eKt+D)=25    ⟺    D+Alim⁡t⟶+∞eKt=25\lim_{t \longrightarrow + \infty} T(t) = 25 \,\,\,\, \Longleftrightarrow \,\,\,\, \lim_{t \longrightarrow + \infty} \left( A \, e^{Kt} + D \right) = 25 \,\,\,\, \Longleftrightarrow \,\,\,\, D + A \lim_{t \longrightarrow + \infty} e^{Kt} = 25
Comme K<0K < 0 on obtient :
D+A×0=25    ⟺    D=25D + A \times 0 = 25 \,\,\,\, \Longleftrightarrow \,\,\,\, D = 25
Ce qui nous donne :
A=75−D    ⟺    A=50    ⟺    T(t)=50 eKt+25A = 75 - D \,\,\,\, \Longleftrightarrow \,\,\,\, A = 50 \,\,\,\, \Longleftrightarrow \,\,\,\, T(t) = 50 \, e^{Kt} + 25
Il nous reste à déterminer la valeur de la constante KK. On sait qu' " après cinq minutes le café est à 50 ∘C50\,^\circ C ". Donc :
T(t=5)=50    ⟺    50 eK5+25=50    ⟺    50 eK5=25    ⟺    e5K=12T(t=5) = 50 \,\,\,\, \Longleftrightarrow \,\,\,\, 50 \, e^{K5} + 25 = 50 \,\,\,\, \Longleftrightarrow \,\,\,\, 50 \, e^{K5} = 25 \,\,\,\, \Longleftrightarrow \,\,\,\, e^{5K} = \dfrac{1}{2}
D'où :
5K=ln⁡(12)    ⟺    5K=−ln⁡(2)    ⟺    K=−ln⁡(2)55K = \ln \left( \dfrac{1}{2} \right) \,\,\,\, \Longleftrightarrow \,\,\,\, 5K = - \ln(2) \,\,\,\, \Longleftrightarrow \,\,\,\, K = - \dfrac{\ln(2)}{5}
Finalement :
T(t)=50 e−ln⁡(2)5t+25{\color{red}{\boxed{T(t) = 50 \, e^{- \frac{\ln(2)}{5} t} + 25}}}
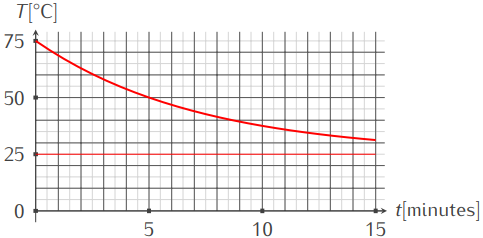
Graphiquement, cela nous donne :

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.