Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
La séparation des variables 3 : en Médecine - Exercice 1
50 min
75
La méthode de constitue une des méthodes les plus puissantes de résolution des équations différentielles ordinaires (EDO). Cette méthode est particulièrement utilisée en Physique.
Soient et deux fonctions continues et non nulles sur un même intervalle. Une équation différentielle est dite à « variables séparées » lorsque l'on a la forme suivante :
Dans ce cas, on obtient :
Ce qui nous permet d'écrire, en , que :
En notant par et les primitives respectives de et , on a alors la solution formelle suivante :
On dit alors que l'équation différentielle considérée est .
Soient et deux fonctions continues et non nulles sur un même intervalle. Une équation différentielle est dite à « variables séparées » lorsque l'on a la forme suivante :
Dans ce cas, on obtient :
Ce qui nous permet d'écrire, en , que :
En notant par et les primitives respectives de et , on a alors la solution formelle suivante :
On dit alors que l'équation différentielle considérée est .
Question 1
On étudie la progression d'une maladie contagieuse dans une population donnée. On note la proportion des personnes malades à l'instant et celle des personnes non atteintes. On a donc, pour , la relation :
On suppose que la vitesse de propagation de la maladie est proportionnelle au produit ; ce qui signifie que .
Si on note le nombre d'individus infectés à l'instant et par le nombre d'individus total, alors il existe une constante réelle telle que :
La ville est isolée et compte individus dont sont malades, et le sont sept jours après.
On suppose que la vitesse de propagation de la maladie est proportionnelle au produit ; ce qui signifie que .
Si on note le nombre d'individus infectés à l'instant et par le nombre d'individus total, alors il existe une constante réelle telle que :
La ville est isolée et compte individus dont sont malades, et le sont sept jours après.
A partir de quel jour l'infection touchera de la population ?
Correction
On a le problème de suivant :
Les solutions constantes sont caractérisées par la condition :
Ensuite, on constate que l'EDO peut s'écrire comme :
On a alors une forme à \og variables séparées \fg. On va donc pouvoir intégrer. On a alors :
Soit :
L'intégration est alors immédiate, et on a alors :
D'où :
Soit encore :
Ainsi, on en déduit que :
Donc :
Ce qui nous donne :
Notons par , et on obtient ainsi :
La condition initiale va nous permettre de déterminer la valeur de la constante réelle . On a alors :
Donc :
Ainsi :
Finalement :
Il nous reste à déterminer la valeur de la constante réelle . Pour cela, utilisons la condition indiquée dans le sujet, à savoir \og le sont sept jours après \fg. On a alors :
Donc :
D'où :
Finalement, la loi d'évolution temporelle de est :
Si de la population est infectée, cela correspond à personnes. Donc . On a alors :
Donc :
Ainsi :
Ce qui nous donne numériquement :
Les solutions constantes sont caractérisées par la condition :
Ensuite, on constate que l'EDO peut s'écrire comme :
On a alors une forme à \og variables séparées \fg. On va donc pouvoir intégrer. On a alors :
Soit :
L'intégration est alors immédiate, et on a alors :
D'où :
Soit encore :
Ainsi, on en déduit que :
Donc :
Ce qui nous donne :
Notons par , et on obtient ainsi :
La condition initiale va nous permettre de déterminer la valeur de la constante réelle . On a alors :
Donc :
Ainsi :
Finalement :
Il nous reste à déterminer la valeur de la constante réelle . Pour cela, utilisons la condition indiquée dans le sujet, à savoir \og le sont sept jours après \fg. On a alors :
Donc :
D'où :
Finalement, la loi d'évolution temporelle de est :
Si de la population est infectée, cela correspond à personnes. Donc . On a alors :
Donc :
Ainsi :
Ce qui nous donne numériquement :
Question 2
A partir de quel jour l'infection touchera de la population ?
Correction
Il est impossible de trouver un nombre de jour fini pour lequel l'infection touche de la population. En fait, mathématiquement, la réponse est l'infinie. Donc :
Graphiquement, on a :
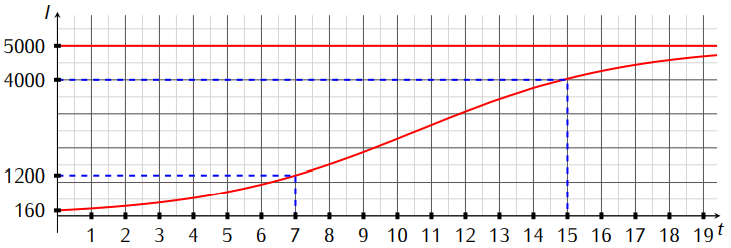
Graphiquement, on a :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.