Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
La méthode de la variation de la constante (5) - Exercice 1
40 min
65
Pour être sûr et certain de savoir appliquer la méthode de la variation de la constante sur une équation différentiel d'ordre un. Voici un exercice un peu plus compliqué.
Question 1
Soit un réel. On considère l'équation différentielle suivante : .
Chercher la solution générale de l'équation différentielle .
Correction
L'équation différentielle est de la forme :
Avec , et .
On a donc :
D'où :
Donc :
Dès lors, on en déduit que :
La solution homogène est donc donnée par :
Soit pour nous :
En ce qui concerne la solution particulière de cette équation différentielle, nous allons poser la forme suivante afin de faire "" :
Par dérivation, on peut écrire que :
Donc l'équation différentielle initiale prend la forme suivante :
Soit :
D'où :
Soit encore :
En simplifiant :
Mais aussi :
Ce qui nous donne :
Donc :
Ce qui nous donne :
On obtient alors :
Finalement :
Donc la solution globale est donnée par la somme :
En factorisant :
Ce qui nous donne :
On pose . Finalement :
Avec , et .
On a donc :
D'où :
Donc :
Dès lors, on en déduit que :
La solution homogène est donc donnée par :
Soit pour nous :
En ce qui concerne la solution particulière de cette équation différentielle, nous allons poser la forme suivante afin de faire "" :
Par dérivation, on peut écrire que :
Donc l'équation différentielle initiale prend la forme suivante :
Soit :
D'où :
Soit encore :
En simplifiant :
Mais aussi :
Ce qui nous donne :
Donc :
Ce qui nous donne :
On obtient alors :
Finalement :
Donc la solution globale est donnée par la somme :
En factorisant :
Ce qui nous donne :
On pose . Finalement :
Question 2
Déterminer la solution qui correspond à la condition initiale .
Correction
Si alors on a . Ce qui nous donne . Ainsi la condition initiale nous donne l'égalité suivante :
.
Soit :
Et de fait, la solution recherchée est donnée par :
Finalement :
Graphiquement, cela nous donne :
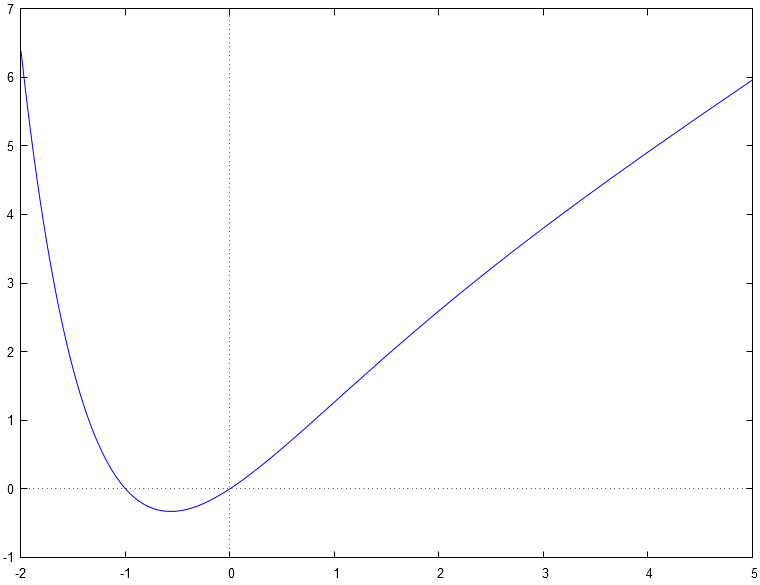
.
Soit :
Et de fait, la solution recherchée est donnée par :
Finalement :
Graphiquement, cela nous donne :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.