Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
La règle du marquis de L'Hôpital - Exercice 1
45 min
70
Calculer les limites proposées ci-dessous.
Question 1
Correction
On constate que cette limite est une forme indéterminée du type .
La fonction présente au numérateur est dérivable, et donc continue, sur .Donc, on a :
Puis, la fonction qui est présente au dénominateur est dérivable, et donc continue, sur l'intervalle . On a alors :
Nous pouvons donc écrire (puisque lorsque cela signifie que ) que :
On remarque que la fonction est définie sur l'intervalle . Donc, dans le calcul de notre limite, tend vers , donc par valeur inférieure à . Donc, posons , avec et . Donc, on obtient :
Ce qui nous donne :
Ce qui nous permet d'écrire que :
De fait, on obtient :
Finalement :
Graphiquement, cela se vérifie :
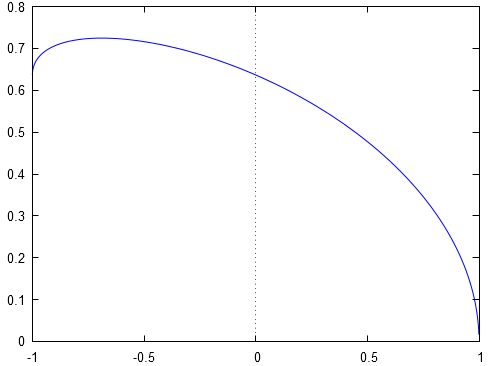
La fonction présente au numérateur est dérivable, et donc continue, sur .Donc, on a :
Puis, la fonction qui est présente au dénominateur est dérivable, et donc continue, sur l'intervalle . On a alors :
Nous pouvons donc écrire (puisque lorsque cela signifie que ) que :
On remarque que la fonction est définie sur l'intervalle . Donc, dans le calcul de notre limite, tend vers , donc par valeur inférieure à . Donc, posons , avec et . Donc, on obtient :
Ce qui nous donne :
Ce qui nous permet d'écrire que :
De fait, on obtient :
Finalement :
Graphiquement, cela se vérifie :

Question 2
Correction
On a une limite qui se présente sous la forme d'une forme indéterminée du type .
La fonction présente au numérateur est dérivable, donc continue, sur . Et on a :
Puis, la fonction présente au dénominateur est dérivable, donc continue, sur . Et on a :
Ainsi, la limite se présente sous la forme d'une forme indéterminée du type . On va donc réitérer la procédure. La fonction présente au numérateur est deux fois dérivable, donc continue, sur . Et on a :
Puis, la fonction présente au dénominateur est deux fois dérivable, donc continue, sur . Et on a :
On en déduit donc que :
Ainsi :
Finalement :
La fonction présente au numérateur est dérivable, donc continue, sur . Et on a :
Puis, la fonction présente au dénominateur est dérivable, donc continue, sur . Et on a :
Ainsi, la limite se présente sous la forme d'une forme indéterminée du type . On va donc réitérer la procédure. La fonction présente au numérateur est deux fois dérivable, donc continue, sur . Et on a :
Puis, la fonction présente au dénominateur est deux fois dérivable, donc continue, sur . Et on a :
On en déduit donc que :
Ainsi :
Finalement :
Question 3
Correction
On a à faire à une forme indéterminée du type .
La fonction du numérateur est dérivable sur , donc y est continue également. De plus :
Puis, la fonction du dénominateur est dérivable sur , donc y est continue également. De plus :
Ceci nous permet d'écrire que :
Donc :
Finalement :
La fonction du numérateur est dérivable sur , donc y est continue également. De plus :
Puis, la fonction du dénominateur est dérivable sur , donc y est continue également. De plus :
Ceci nous permet d'écrire que :
Donc :
Finalement :
Question 4
Correction
On note . On constate que .
La limite étudiée est une forme indéterminée du type .
La fonction est dérivable, donc continue, sur . On a alors :
Puis, la fonction est dérivable, donc continue, sur . On a alors :
De fait, la limite est également une forme indéterminée du type . On va reconduire la procédure.
La fonction est deux fois dérivable, donc continue, sur . On a alors :
Puis, la fonction est deux fois dérivable, donc continue, sur . On a alors :
Ce qui nous donne :
Ce qui nous permet d'écrire :
Donc, on obtient :
Dès lors :
Puis :
Finalement :
En effet, graphiquement, on a :
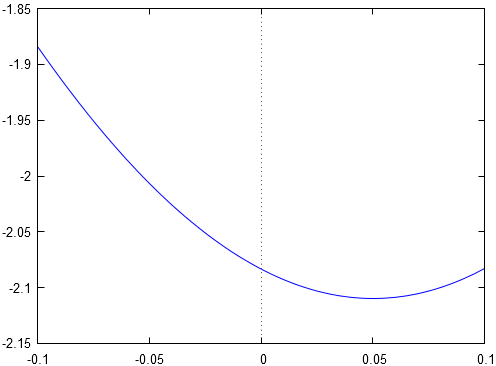
La limite étudiée est une forme indéterminée du type .
La fonction est dérivable, donc continue, sur . On a alors :
Puis, la fonction est dérivable, donc continue, sur . On a alors :
De fait, la limite est également une forme indéterminée du type . On va reconduire la procédure.
La fonction est deux fois dérivable, donc continue, sur . On a alors :
Puis, la fonction est deux fois dérivable, donc continue, sur . On a alors :
Ce qui nous donne :
Ce qui nous permet d'écrire :
Donc, on obtient :
Dès lors :
Puis :
Finalement :
En effet, graphiquement, on a :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.