Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Dérivations partielles - Exercice 1
1 h
90
Pour les fonctions proposées, déterminer les dérivées partielles par rapport à toutes les variables, puis écrire l'expression de la différentielle associée .
Question 1
Soit
Sur le pavé la surface représentative de est :
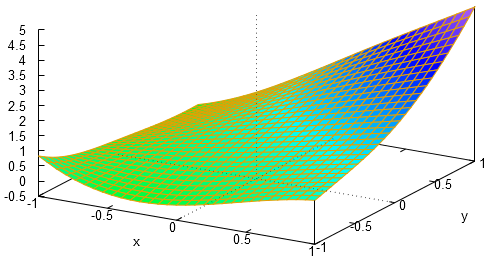
Sur le pavé la surface représentative de est :

Correction
On a la dérivée partielle, par rapport à la variable , suivante :
Soit :
Soit encore :
Comme et que , on en déduit que :
Soit encore :
D'où :
Finalement, on obtient :
Puis, on a la dérivée partielle, par rapport à la variable , suivante :
Soit :
Avec , on obtient :
D'où :
Finalement, on obtient :
La différentielle est donc donnée par l'expression suivante :
Soit :
Soit encore :
Comme et que , on en déduit que :
Soit encore :
D'où :
Finalement, on obtient :
Puis, on a la dérivée partielle, par rapport à la variable , suivante :
Soit :
Avec , on obtient :
D'où :
Finalement, on obtient :
La différentielle est donc donnée par l'expression suivante :
Question 2
Soit
Correction
On a la dérivée partielle, par rapport à la variable , suivante :
Soit :
Dans l'expression la puissance est indépendante de , donc Puis, dans les termes et les puissances dépendes de , c'est pourquoi :
De même :
On obtient alors :
Soit encore :
On a encore :
En utilisant des propriétés de la fonction logarithme naturel, on obtient finalement :
On a la dérivée partielle, par rapport à la variable , suivante :
On a donc :
Puis :
De même :
Ce qui nous donne :
Soit encore :
En factorisant par , on obtient :
En faisant usages des propriétés du logarithme, on obtient finalement :
On a la dérivée partielle, par rapport à la variable , suivante :
On a donc :
Puis :
De même :
Ce qui nous donne :
Soit encore :
En factorisant par , on obtient :
En faisant usages des propriétés du logarithme, on obtient finalement :
Ainsi, la différentielle prend l'expression suivante :
Finalement :
Soit :
Dans l'expression la puissance est indépendante de , donc Puis, dans les termes et les puissances dépendes de , c'est pourquoi :
De même :
On obtient alors :
Soit encore :
On a encore :
En utilisant des propriétés de la fonction logarithme naturel, on obtient finalement :
On a la dérivée partielle, par rapport à la variable , suivante :
On a donc :
Puis :
De même :
Ce qui nous donne :
Soit encore :
En factorisant par , on obtient :
En faisant usages des propriétés du logarithme, on obtient finalement :
On a la dérivée partielle, par rapport à la variable , suivante :
On a donc :
Puis :
De même :
Ce qui nous donne :
Soit encore :
En factorisant par , on obtient :
En faisant usages des propriétés du logarithme, on obtient finalement :
Ainsi, la différentielle prend l'expression suivante :
Finalement :
Question 3
Soit
Correction
On a la dérivée partielle de , par rapport à la variable , suivante :
Soit :
Donc :
Finalement :
Les rôles parfaitement symétriques des quatre variables , , et , nous permettent d'écrire que :
Donc, la différentielle prend la forme suivante :
En factorisant par , on obtient :
Soit :
Donc :
Finalement :
Les rôles parfaitement symétriques des quatre variables , , et , nous permettent d'écrire que :
Donc, la différentielle prend la forme suivante :
En factorisant par , on obtient :
Question 4
Soit
Correction
La dérivée partielle de par rapport à est donnée par :
Soit :
Soit encore :
Ce qui nous donne :
Avec :
Ce qui nous donne donc :
Puis :
On en déduit alors que :
Ainsi, on obtient :
Finalement :
La dérivée partielle de par rapport à est donnée par :
Soit :
Soit encore :
Avec :
Puis :
Soit :
Soit encore :
On obtient alors :
Finalement :
La dérivée partielle de par rapport à est donnée par :
Soit :
Soit encore :
Qui s'écrit encore comme :
Où encore :
Ce qui nous donne :
Avec :
Dès lors, l'expression de la dérivée partielle de , par rapport à , devient :
De même :
Finalement :
La dérivée partielle de par rapport à est donnée par :
Soit :
Soit encore :
De même :
Ou encore :
On obtient alors :
Comme :
Finalement, en factorisant par , on trouve que :
La différentielle prend donc la forme suivante :
Soit :
Soit encore :
Ce qui nous donne :
Avec :
Ce qui nous donne donc :
Puis :
On en déduit alors que :
Ainsi, on obtient :
Finalement :
La dérivée partielle de par rapport à est donnée par :
Soit :
Soit encore :
Avec :
Puis :
Soit :
Soit encore :
On obtient alors :
Finalement :
La dérivée partielle de par rapport à est donnée par :
Soit :
Soit encore :
Qui s'écrit encore comme :
Où encore :
Ce qui nous donne :
Avec :
Dès lors, l'expression de la dérivée partielle de , par rapport à , devient :
De même :
Finalement :
La dérivée partielle de par rapport à est donnée par :
Soit :
Soit encore :
De même :
Ou encore :
On obtient alors :
Comme :
Finalement, en factorisant par , on trouve que :
La différentielle prend donc la forme suivante :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.