Vecteurs du plan : deuxième partie Géométrie analytique . Coordonnées des vecteurs dans une base orthonormée
Exercices Types - Exercice 1
20 min
35
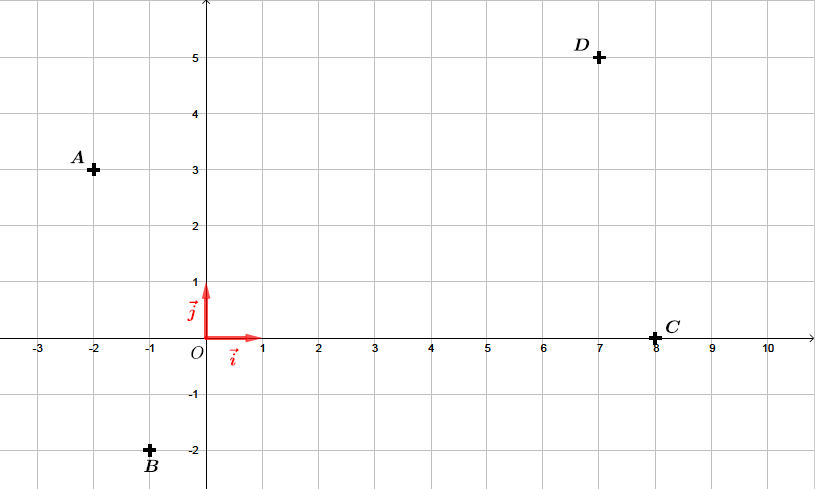
Dans un repère orthonormé , on donne les points , , et .
Question 1
Faire une figure.
Correction
Question 2
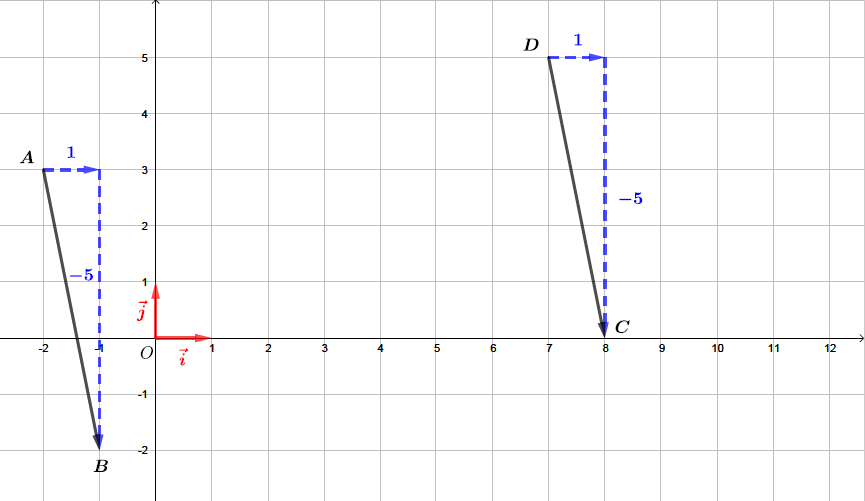
Calculer les coordonnées des vecteurs et .
Correction
Question 3
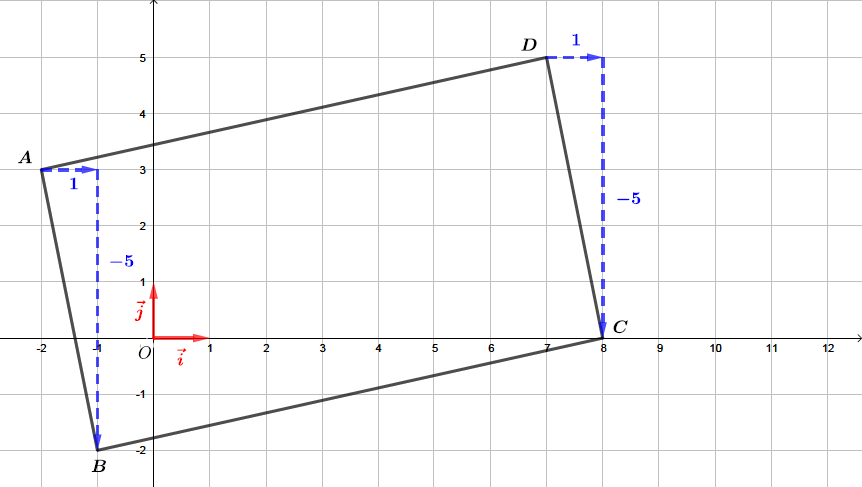
Que peut-on en déduire? justifier.
Correction
Soit un repère du plan et quatre points ; ; et
Comme alors le quadrilatère est un parallélogramme.- Le quadrilatère est un parallélogramme si et seulement si . Autrement dit, il faut vérifier que deux vecteurs opposées soient égaux.
Question 4
Calculer les longueurs et .
Correction
Soit un repère orthonormal du plan et deux points et . La distance est donnée par la formule :
D'une part : équivaut successivement à :
D'autre part :
équivaut successivement à :
Question 5
Calculer les coordonnées du point tel que
Correction
Notons les coordonnées du point recherché. Commençons par calculer les vecteurs et .
ainsi d'où :
ainsi d'où :
Or nous savons que : .
Il vient alors que :
On obtient alors deux équations à résoudre. Nous l'écrivons sous forme de système.
Ainsi :
Les coordonnées du point sont alors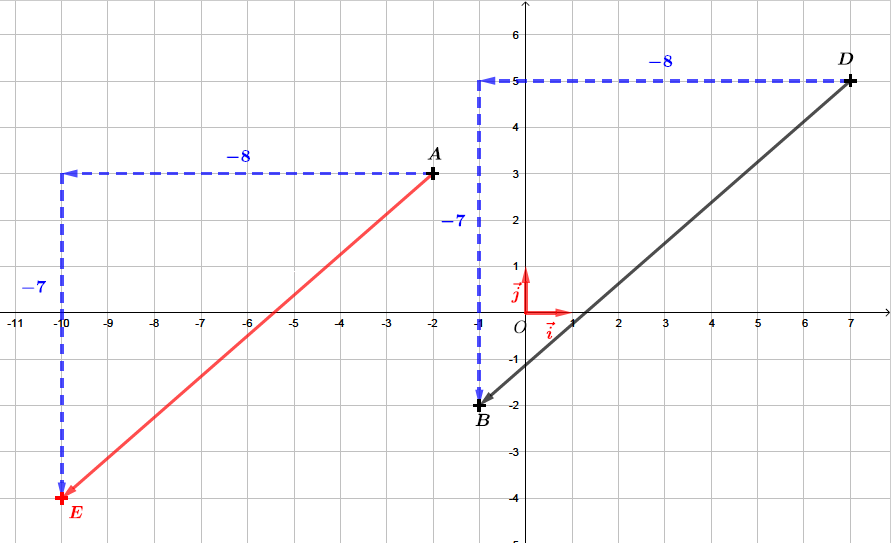
ainsi d'où :
ainsi d'où :
Or nous savons que : .
Il vient alors que :
On obtient alors deux équations à résoudre. Nous l'écrivons sous forme de système.
Ainsi :
Les coordonnées du point sont alors
