Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Théorème de Pythagore : cas où on cherche l'un des côtés perpendiculaires - Exercice 4

5 min
10
COMPETENCE :
1°) Extraire des informations, les organiser, les confronter à ses connaissances.
2°) Utiliser un raisonnement logique et des règles établies (théorèmes) pour parvenir à une conclusion.
Question 1
LKJLKJ est un triangle rectangle en JJ avec KL=58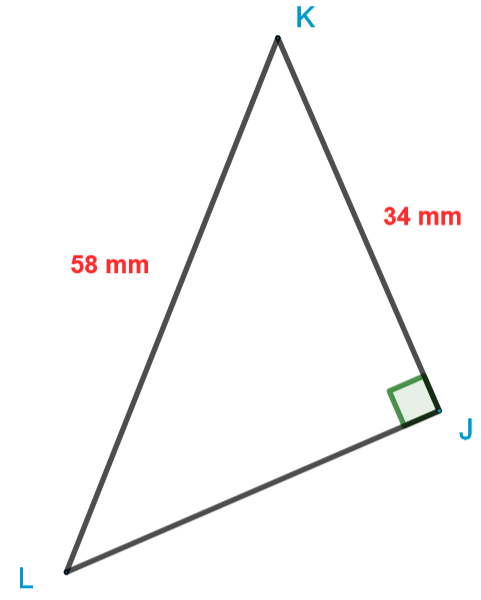KL = 58 mm et KJ=34KJ = 34 mm.

Calculer LJLJ. Donner la valeur exacte et la valeur approchée à 10−210^{-2} près.

Correction
Comme le triangle LKJLKJ est rectangle en JJ avec KL=58KL = 58 mm et KJ=34KJ = 34 mm . On peut appliquer le théorème de Pythagore :
KL2=KJ2+JL2KL^{2} =KJ^{2} +JL^{2}
  • (Le coˆteˊ que l’on recherche\text{Le côté que l'on recherche})2^{2} == (l’hypoteˊnuse\text{l'hypoténuse})2^{2} −- (le coteˊ que l’on connait\text{le coté que l'on connait} )2^{2} .
On a alors :
JL2=KL2−KJ2JL^{2} =KL^{2} -KJ^{2}
JL2=582−342JL^{2} =58^{2} -34^{2}
JL2=3364−1156JL^{2} =3364-1156
JL2=2208JL^{2} =2208 . Nous allons utiliser la racine carrée pour déterminer la mesure de JLJL.
D'où :
JL=2208  cm\color{blue}\boxed{JL=\sqrt{2208}\;cm}. Il s'agit de la valeur exacte.
JL≈46,99  cm\color{blue}\boxed{JL\approx46,99\;cm} . Il s'agit de la valeur approchée à 10−210^{-2} près.

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.