Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Savoir résoudre des problèmes se ramenant à des équations du premier degré - Exercice 1
12 min
25
COMPETENCES:
1°) Résoudre des problèmes, analyser et exploiter ses erreurs.
2°) Savoir résoudre une équation et calculer en utilisant le langage algébrique. (Lettres, symboles, etc).
1°) Résoudre des problèmes, analyser et exploiter ses erreurs.
2°) Savoir résoudre une équation et calculer en utilisant le langage algébrique. (Lettres, symboles, etc).
Question 1
Considérons le carré ci-dessous :
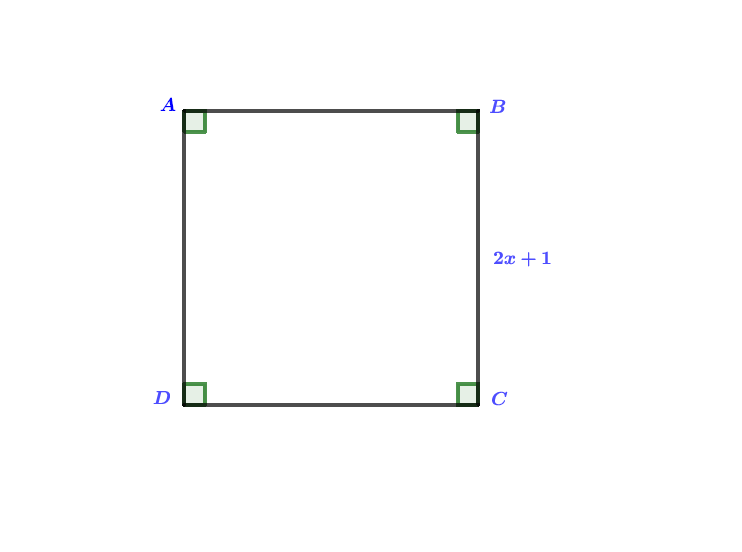

Pour quelle valeur de le périmètre du carré est de
Correction
Le carré à côtés de même longueur. Donc son périmètre est :
Ici on sait que . Par conséquent :
.
.
.
Or dans l'énoncé on sait que le périmètre du carré est de .
On doit donc ici résoudre l'équation suivante
On soustrait à chaque membre .
. On divise chaque membre par le nombre devant le qui ici vaut .
Ainsi :
On peut donc conclure que pour , le périmètre du carré ABCD est de .
Ici on sait que . Par conséquent :
.
.
.
Or dans l'énoncé on sait que le périmètre du carré est de .
On doit donc ici résoudre l'équation suivante
On soustrait à chaque membre .
. On divise chaque membre par le nombre devant le qui ici vaut .
Ainsi :
On peut donc conclure que pour , le périmètre du carré ABCD est de .
Question 2
Considérons le triangle ci-dessous :
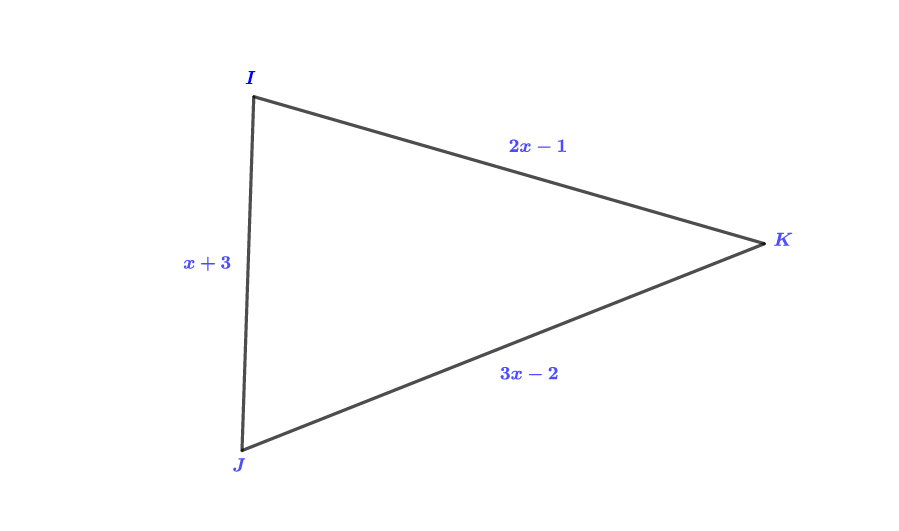

Pour quelle valeur de le périmètre du triangle est de
Correction
Le périmètre du triangle est : .
.
. Ici on peut supprimer les parenthèses car elles sont précédées d'un signe .
.
Or dans l'énoncé on sait que le périmètre du triangle est de .
On doit donc ici résoudre l'équation suivante
. On divise chaque membre par le nombre devant le qui ici vaut .
Ainsi :
On peut donc conclure que pour le périmètre du triangle IJK est de .
.
. Ici on peut supprimer les parenthèses car elles sont précédées d'un signe .
.
Or dans l'énoncé on sait que le périmètre du triangle est de .
On doit donc ici résoudre l'équation suivante
. On divise chaque membre par le nombre devant le qui ici vaut .
Ainsi :
On peut donc conclure que pour le périmètre du triangle IJK est de .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.