Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Sujet 3 - Exercice 1

10 min
20
Question 1
Leila est en visite à Paris. Aujourd’hui, elle est au Champ de Mars où elle peut voir la tour Eiffel dont la hauteur totale BHBH est 324  m324\;m.
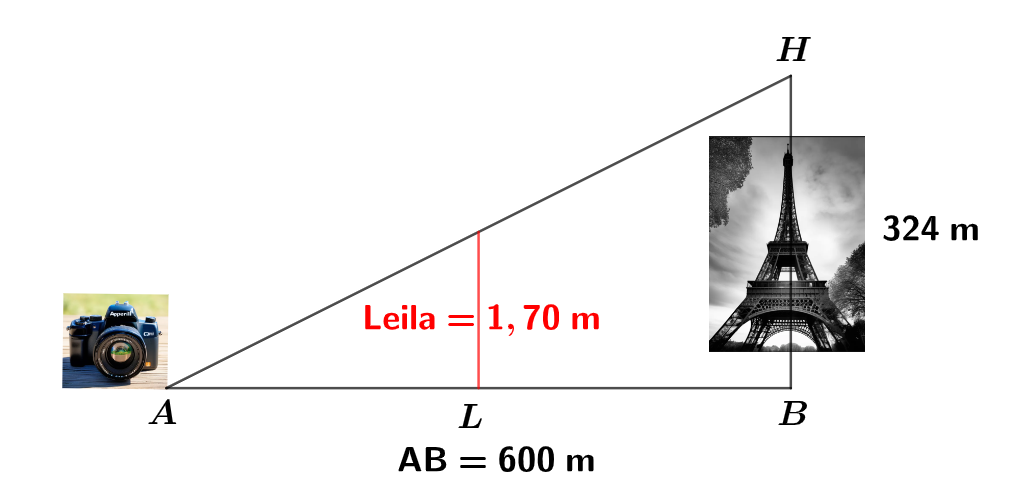
Elle pose son appareil photo au sol à une distance AB=600  mAB = 600\;m du monument et le programme pour prendre une photo (voir le dessin ci-dessous).

Quelle est la mesure, au degré près, de l’angle HAB^\widehat{HAB} ??

Correction
Ici, on suppose que la tour Eiffel est perpendiculaire au sol.
Le triangle ABHABH est rectangle en BB. Nous connaissons :
  • Le côté opposé à l'angle A^\widehat{A} dont la mesure est BH=324  mBH=324\;m.
  • Le côté adjacent à l'angle A^\widehat{A} dont la mesure est BA=600  mBA=600\;m.
  • Nous recherchons l'angle A^\widehat{A}.
    • Nous allons donc utiliser la tangente{\color{blue}\text{tangente}}.
    tan⁡(HAB^)=coteˊ opposeˊ aˋ l’angle A^coteˊ adjacent aˋ l’angle A^\tan\left(\widehat{HAB}\right)=\frac{\text{coté opposé à l'angle }\widehat{A}}{\text{coté adjacent à l'angle }\widehat{A}}
    tan⁡(HAB^)=BHBA\tan\left(\widehat{HAB}\right)=\frac{BH}{BA}
    tan⁡(HAB^)=324600\tan\left(\widehat{HAB}\right)=\frac{324}{600}
    HAB^=tan⁡−1(324600)\widehat{HAB}=\tan^{-1}\left(\frac{324}{600}\right) ou encore HAB^=arctan(324600)\widehat{HAB}=\text{arctan}\left(\frac{324}{600}\right)
    • Il faut vérifier que votre calculatrice est bien en mode degré, et n'oubliez pas de mettre les parenthèses.
    Ainsi :
    HAB^≈28,36∘\widehat{HAB}\approx28,36{}^\circ

    La mesure de l'angle HAB^\widehat{HAB} est de 28∘28{}^\circ (arrondi au degré près).
    Question 2

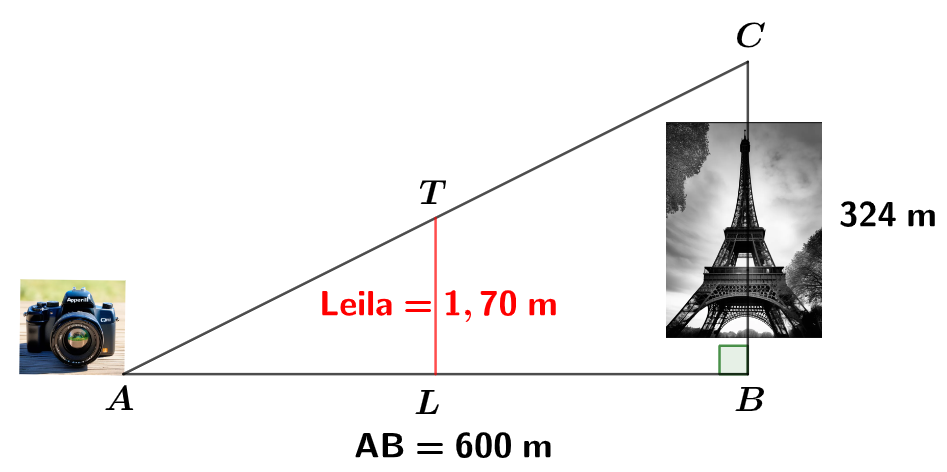
    Sachant que Leila mesure 1,70  m1,70\;m, à quelle distance ALAL doit-elle se placer pour paraître aussi grande que la tour Eiffel sur sa photo ??
    Donne une valeur approchée du résultat au centimètre près.

    Correction
    Le point TT est le point sur lequel se situe la tête de Leila.
  • Les points AA, TT et CC sont alignés dans le même ordre que les points AA, LL et BB.
  • Les droites (TL)\left(TL\right) et (CB)\left(CB\right) sont parallèles.
    • En effet, les droites (TL)(TL) et (CB)(CB) sont toutes les deux perpendiculaires à la même droite (AB)(AB), elles sont donc parallèles.
    D'après le théorème de Thalès, on a :
    ATAC=ALAB=TLCB\frac{AT}{AC} =\frac{AL}{AB} =\frac{TL}{CB}. Nous allons remplacer par les mesures. Ainsi :
    ATAC=AL600=1,70324\frac{AT}{AC} =\frac{AL}{600} =\frac{1,70}{324}
    À partir de AL600=1,70324\frac{AL}{600} =\frac{1,70}{324} on effectue un produit en croix. Cela nous donne :
    AL=1,70×600324AL=\frac{1,70\times 600}{324}
    AL≈3,15AL\approx 3,15 m

    On peut donc conclure, que Leila doit se placer à environ 3,15  m3,15\;m du point AA.

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.