Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Sujet 1 - Exercice 1
13 min
25
Adrien veut installer chez lui un panier de basket. Il doit le fixer à m du sol. L’échelle dont il se sert mesure m de long.
On a schématisé la situation à l'aide de la figure ci-dessous.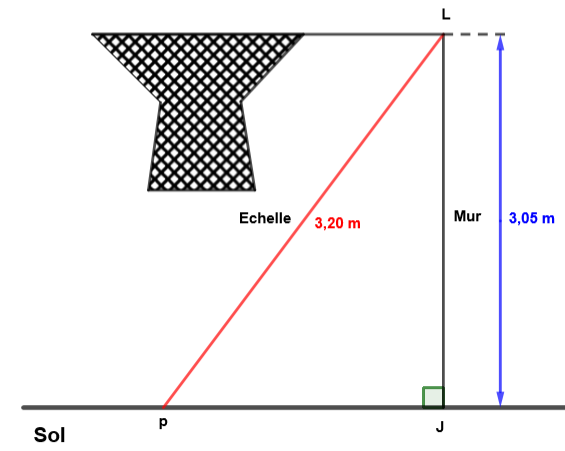
On a schématisé la situation à l'aide de la figure ci-dessous.

Question 1
À quelle distance du pied du mur doit-il placer l'échelle pour que son sommet soit juste au niveau du panier ?
(Donner une valeur approchée au dixième près).
(Donner une valeur approchée au dixième près).
Correction
Ici, il nous faut calculer la longueur .
Comme le triangle est rectangle en avec m et m. On peut appliquer le théorème de Pythagore :
On a alors :
. Nous allons utiliser la racine carrée pour déterminer la mesure de .
D'où :
Ainsi :
Ici, on peut convertir la longueur en cm, soit m = cm
La mesure de est donc de cm. (arrondie au dixième près).
On en déduit donc que l'échelle doit être placée à cm du pied du mur pour que son sommet soit juste au niveau du panier.
Comme le triangle est rectangle en avec m et m. On peut appliquer le théorème de Pythagore :
- () () ().
. Nous allons utiliser la racine carrée pour déterminer la mesure de .
D'où :
Ainsi :
m
Ici, on peut convertir la longueur en cm, soit m = cm
cm
La mesure de est donc de cm. (arrondie au dixième près).
On en déduit donc que l'échelle doit être placée à cm du pied du mur pour que son sommet soit juste au niveau du panier.
Question 2
Déterminer la mesure arrondie au degré près de l'angle .
Correction

ou encore
- Il faut vérifier que votre calculatrice est bien en mode degré, et n'oubliez pas de mettre les parenthèses.
La mesure de l'angle est de (arrondie au degré près).
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.