Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Déterminer la mesure d'un angle à l'aide de tangente - Exercice 5

5 min
10
COMPETENCE :
1°) Extraire des informations, les organiser, les confronter à ses connaissances.
2°) Utiliser un raisonnement logique et des règles établies (théorèmes) pour parvenir à une conclusion.
Question 1

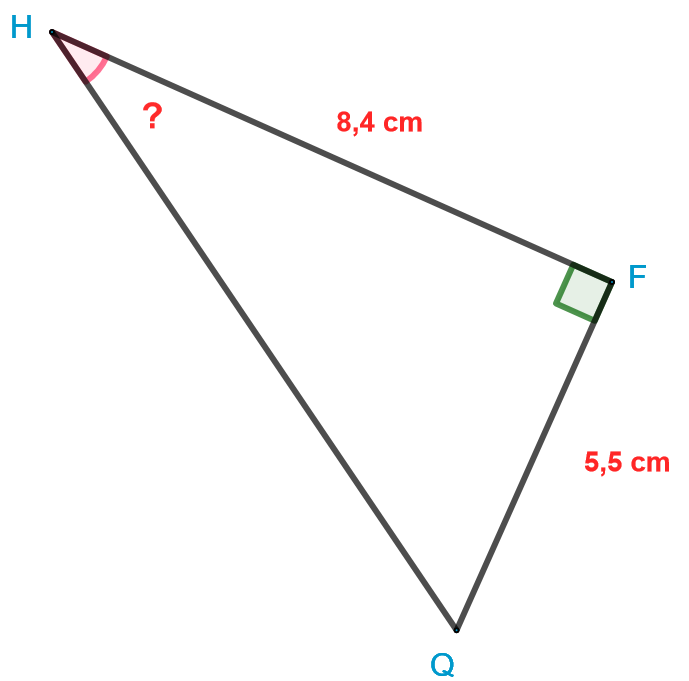
Donner une mesure de l'angle QHF^\widehat{QHF} au dixième près.

Correction
Le triangle HFQHFQ est rectangle en FF. Nous connaissons :
  • Le côté opposé à l'angle H^\widehat{H} dont la mesure est FQ=5,5FQ=5,5 cm.
  • Le côté adjacent à l'angle H^\widehat{H} dont la mesure est FH=8,4FH=8,4 cm.
  • Nous recherchons l'angle H^\widehat{H}.
    • Nous allons donc utiliser la tangente{\color{blue}\text{tangente}}.
    tan⁡(QHF^)=coteˊ opposeˊ aˋ l’angle H^coteˊ adjacent aˋ l’angle H^\tan\left(\widehat{QHF}\right)=\frac{\text{coté opposé à l'angle }\widehat{H}}{\text{coté adjacent à l'angle }\widehat{H}}
    tan⁡(QHF^)=FQFH\tan\left(\widehat{QHF}\right)=\frac{FQ}{FH}
    tan⁡(QHF^)=5,58,4\tan\left(\widehat{QHF}\right)=\frac{5,5}{8,4}
    QHF^=tan⁡−1(5,58,4)\widehat{QHF}=\tan^{-1}\left(\frac{5,5}{8,4}\right) ou encore QHF^=arctan(5,58,4)\widehat{QHF}=\text{arctan}\left(\frac{5,5}{8,4}\right)
    • Il faut vérifier que votre calculatrice est bien en mode degré, et n'oubliez pas de mettre les parenthèses.
    Ainsi :
    QHF^≈33,21∘\widehat{QHF}\approx33,21{}^\circ

    La mesure de l'angle QHF^\widehat{QHF} est de 33,2∘33,2{}^\circ (arrondi au dixième près).

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.