Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Sujet 1 - Exercice 1
20 min
40
Question 1
La figure ci-dessous n'est pas représentée en vraie grandeur.
Les points et sont alignés.
Le triangle est rectangle en
Le triangle est rectangle en 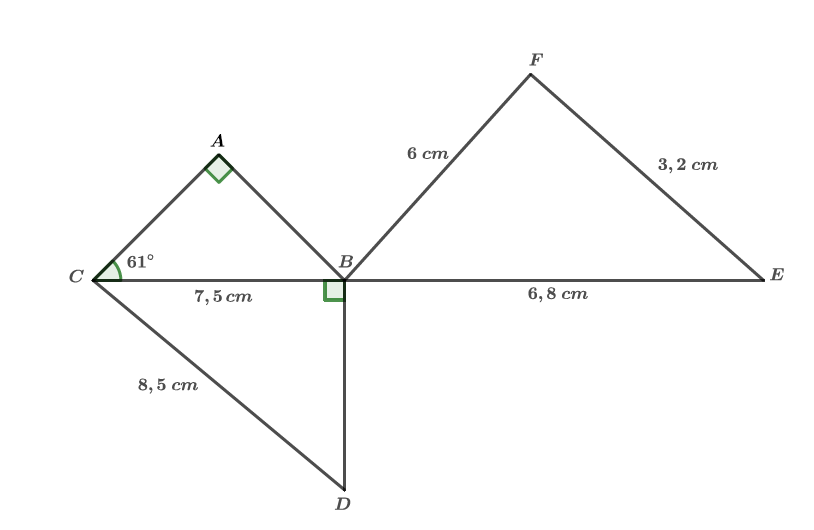

Montrer que la longueur est égale à
Correction
Comme le triangle est rectangle en avec cm et cm. On peut appliquer le théorème de Pythagore :
On a alors :
. Nous allons utiliser la racine carrée pour déterminer la mesure de .
D'où :
.
- () () () .
. Nous allons utiliser la racine carrée pour déterminer la mesure de .
D'où :
.
Question 2
Montrer que les triangles et sont semblables.
Correction
- Si deux triangles ont leurs côtés proportionnels alors ce sont deux triangles semblables.
Calculons dans un second temps:
Et dans un troisième temps:
On constate ici que :
Par conséquent, on peut conclure que les triangles CBD et BFE sont semblables.
Question 3
Sophie affirme que l’angle est un angle droit. A-t-elle raison ?
Correction
À la question précédente, on a démontré que les triangles et étaient semblables.
Par conséquent, on a :
Or le triangle est rectangle en , on peut donc en déduire que
On peut donc conclure que Sophie a raison.
- Deux triangles semblables sont deux triangles qui ont leurs angles deux à deux de même mesure.
Or le triangle est rectangle en , on peut donc en déduire que
On peut donc conclure que Sophie a raison.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.