Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Exercices types : 2ème partie - Exercice 2

10 min
25
Question 1
On considère la figure ci-dessous :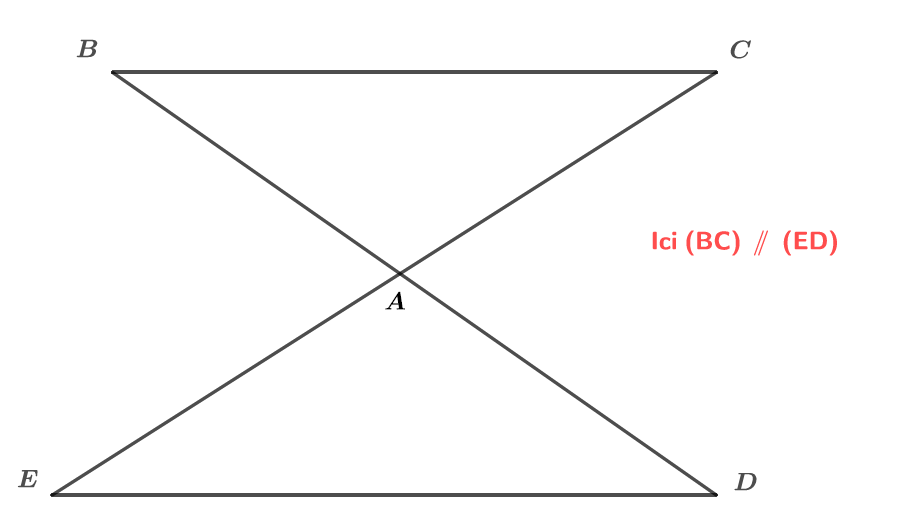

Justifier que les angles EAD^\widehat{EAD} et BAC^\widehat{BAC} sont de la même mesure.

Correction
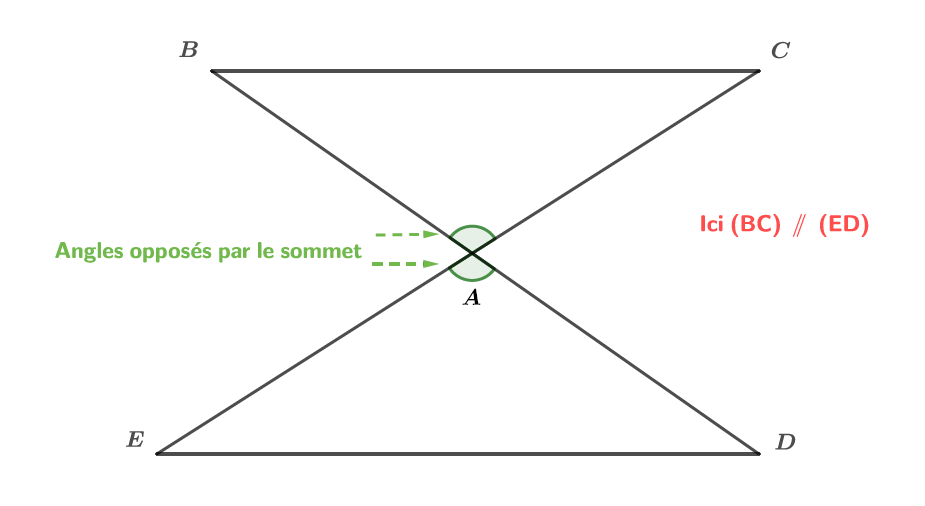
D'après la figure ci-dessus, on constate que :
  • Les angles EAD^\widehat{EAD} et BAC^\widehat{BAC} sont opposés par le sommet.
    • Or deux angles opposés par le sommet ont la même mesure.
    On en déduit donc que les angles EAD^\widehat{EAD} et BAC^\widehat{BAC} sont de la même mesure.
    • Question 2

    Justifier que les angles ABC^\widehat{ABC} et ADE^\widehat{ADE} sont de la même mesure.

    Correction
    D'après la figure ci-dessus, on constate que :
  • Les angles ABC^\widehat{ABC} et ADE^\widehat{ADE} sont alternes internes.
  • Les droites (BC)(BC) et (ED)(ED) sont parallèles.
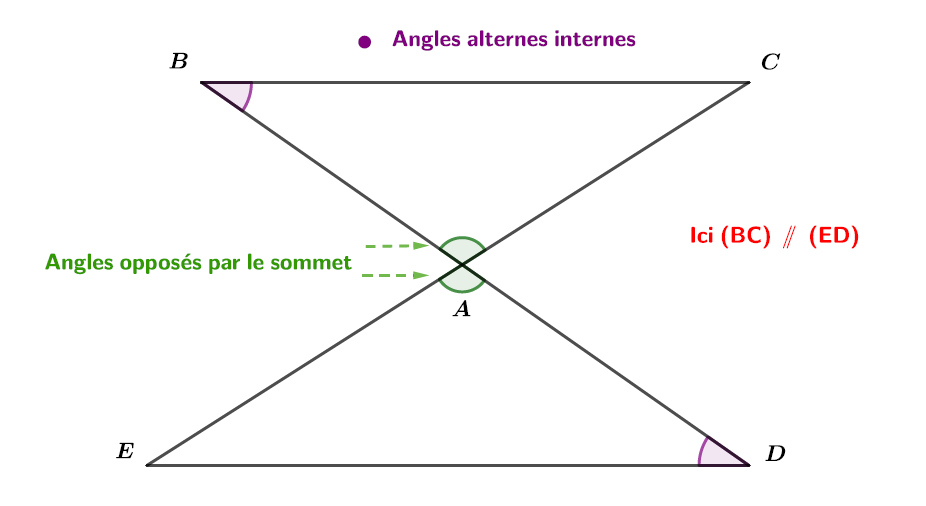
    Si deux droites parallèles sont coupées par une sécante, alors elles forment des angles alternes-internes deux à deux de même mesure.
    On en déduit donc que les angles ABC^\widehat{ABC} et ADE^\widehat{ADE} sont de la même mesure.
    • Question 3

    En déduire que les triangles ABCABC et ADEADE sont semblables.

    Correction
    Des questions précédentes, on sait que :
  • Les angles EAD^\widehat{EAD} et BAC^\widehat{BAC} sont de la même mesure.
  • Les angles ABC^\widehat{ABC} et ADE^\widehat{ADE} sont de la même mesure.
    Si deux triangles ont seulement deux paires d'angles de même mesure, alors ils sont semblables.
    On peut donc conclure que les triangles ABC et ADE ont deux paires d'angles de la même mesure, ils sont donc semblables.

    • Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.