Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Sujet 2 - Exercice 1
1 min
0
Question 1
Dans cet exercice, on considère la figure codée ci-dessous :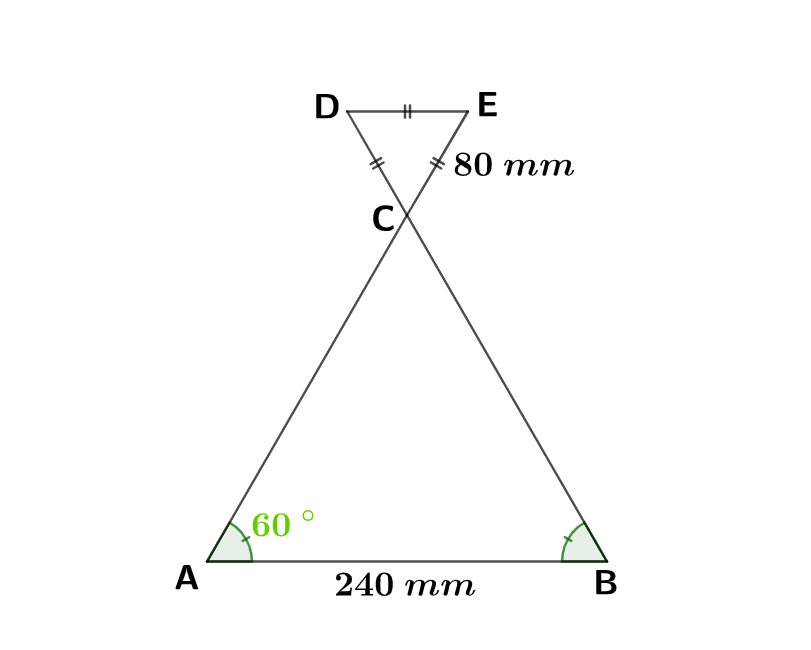
Les points et sont alignés.
Les points et sont alignés.

Les points et sont alignés.
Les points et sont alignés.
Partie A
Montrer que le triangle est équilatéral.
Montrer que le triangle est équilatéral.
Correction
Dans le triangle on sait d'après le codage que
Les trois angles du triangle mesurent , on peut donc conclure que le triangle est équilatéral.
- Dans un triangle, la somme des trois angles est égale à
Les trois angles du triangle mesurent , on peut donc conclure que le triangle est équilatéral.
Question 2
Montrer que les droites et sont parallèles.
Correction
Calculons d'autre part :
On constate ici, que : .
Donc d’après la réciproque du théorème de Thalès les droites et sont parallèles.
Question 3
Partie B
On donne le programme suivant qui permet de tracer la figure précédente.
Ce programme comporte une variable nommée « côté ».
Les longueurs sont données en pas : pas représente
On rappelle que l’instruction signifie que le lutin se dirige horizontalement vers la droite.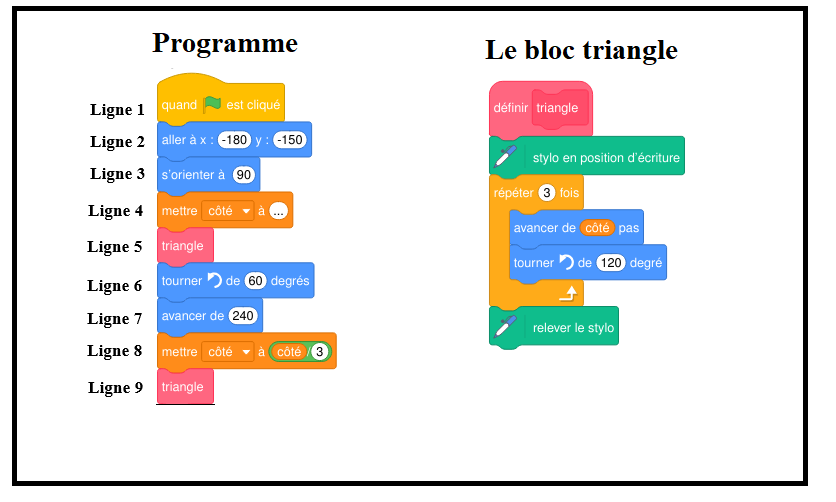
On donne le programme suivant qui permet de tracer la figure précédente.
Ce programme comporte une variable nommée « côté ».
Les longueurs sont données en pas : pas représente
On rappelle que l’instruction signifie que le lutin se dirige horizontalement vers la droite.

Quelles sont les coordonnées du point de départ du lutin ? Aucune justification n’est demandée.
Correction
Comme on peut le constater au début du programme, les coordonnées de départ sont : .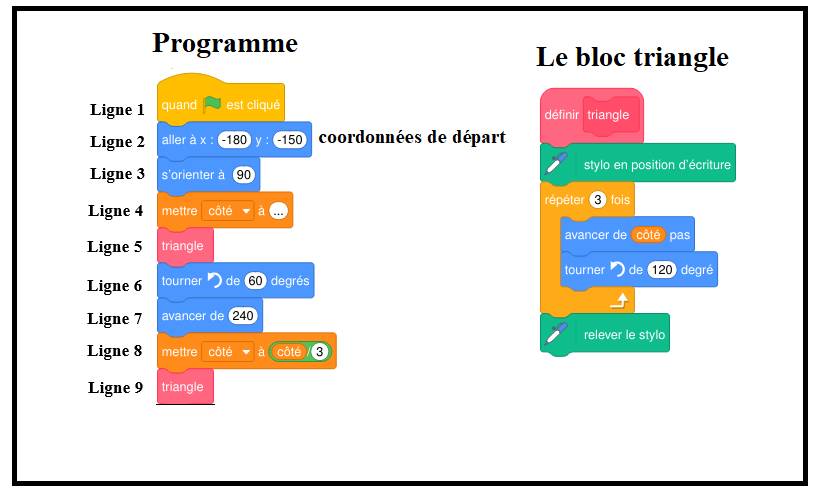

Question 4
Quelle valeur doit être saisie à la ligne dans le programme ? Aucune justification n’est demandée.
Correction
Au départ, le lutin va commencer à tracer le triangle équilatéral .
Donc au départ, il devra commencer à tracer le côté de ce triangle, , c'est-à-dire .
Donc au départ, il devra commencer à tracer le côté de ce triangle, , c'est-à-dire .
Question 5
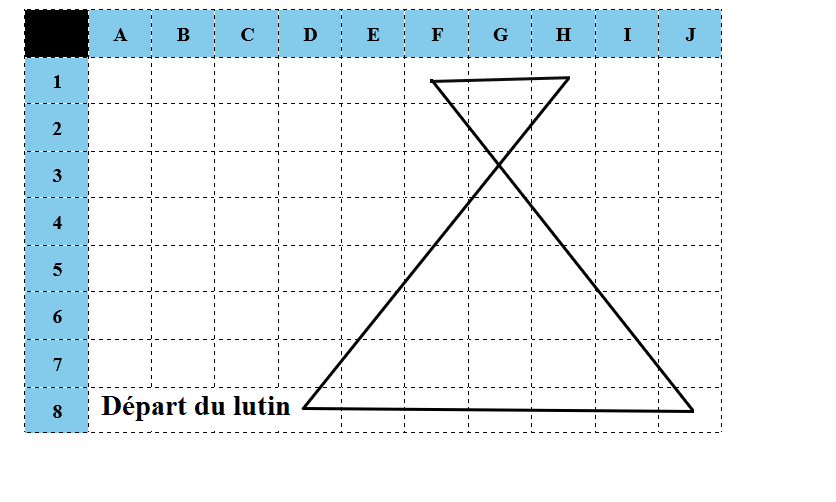 Le lutin démarre à la case D8. Dans quelle case se trouve-t-il lorsqu’il vient d’exécuter la ligne du programme Aucune justification n’est demandée.
Le lutin démarre à la case D8. Dans quelle case se trouve-t-il lorsqu’il vient d’exécuter la ligne du programme Aucune justification n’est demandée.

Correction
Après l’exécution de la ligne , le lutin se trouve au point de coordonnées .
Question 6
Expliquer l’instruction « côté » de la ligne du programme pour le tracé de la figure
Correction
On sait que le triangle est un triangle équilatéral qui a pour longueur de côté, c'est-à-dire un côté trois fois plus petit que le triangle équilatéral .
En effet : qui est longueur du petit triangle.
En effet : qui est longueur du petit triangle.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.