Qui aura 20 en maths ?

💯 Le grand concours 100% Terminale revient le 31 mai 2026 en ligne !Découvrir →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →

S'approprier le théorème de Thalès - Exercice 1

5 min

COMPÉTENCE :
1°) Extraire des informations, les organiser, les confronter à ses connaissances.
2°) Utiliser un raisonnement logique et des règles établies (théorèmes) pour parvenir à une conclusion.

Question 1

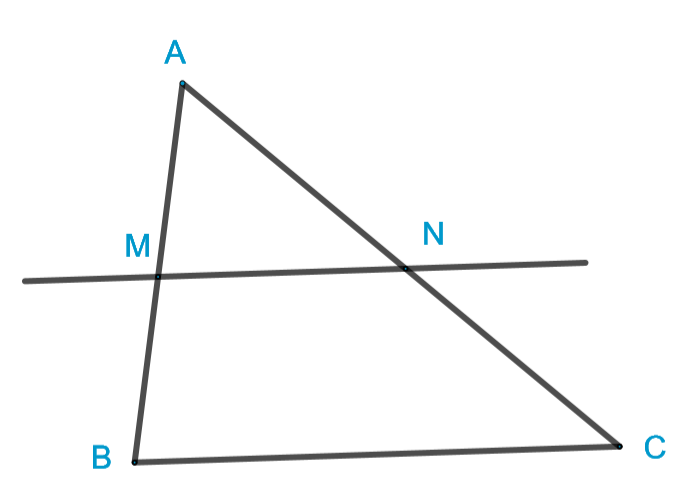
On donne la figure ci-dessus en sachant que les droites $\left(MN\right)$ et $\left(BC\right)$ sont parallèles.
De plus : $AB = 5$ cm, $AC= 7$ cm, $AM = 2$ cm.
Déterminer la mesure du segment $\left[AN\right]$ .

Correction

Les points $A$ , $M$ et $B$ sont alignés dans le même ordre que les points $A$ , $N$ et $C$ .

Les droites $\left(MN\right)$ et $\left(BC\right)$ sont parallèles.

D'après le théorème de Thalès, on a :

\frac{AM}{AB} =\frac{AN}{AC} =\frac{MN}{BC}

. Nous allons remplacer par les mesures. Ainsi :

\frac{2}{5} =\frac{AN}{7} =\frac{MN}{BC}

À partir de

\frac{2}{5} =\frac{AN}{7}

on effectue un produit en croix. Cela nous donne :

AN=\frac{2\times 7}{5}

AN=2,8

La mesure du segment $\left[AN\right]$ est de $2,8$ cm.

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.

S'approprier le théorème de Thalès - Exercice 1

On donne la figure ci-dessus en sachant que les droites (MN)\left(MN\right)(MN) et (BC)\left(BC\right)(BC) sont parallèles. De plus : AB=5AB = 5AB=5 cm, AC=7AC= 7AC=7 cm, AM=2AM = 2AM=2 cm. Déterminer la mesure du segment [AN]\left[AN\right][AN].

On donne la figure ci-dessus en sachant que les droites $\left(MN\right)$ et $\left(BC\right)$ sont parallèles.
De plus : $AB = 5$ cm, $AC= 7$ cm, $AM = 2$ cm.
Déterminer la mesure du segment $\left[AN\right]$ .