Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Savoir déterminer une médiane lorsque l'effectif de la série est pair - Exercice 1
6 min
15
COMPETENCES : Calculer et interpréter des caractéristiques de position ou de dispersion d’une série statistique.
Question 1
On définit la série statistique suivante :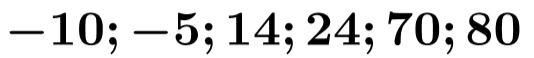
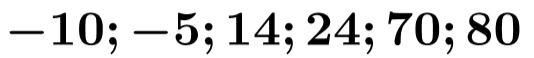
Quelle est la médiane de cette série?
Correction
Dans un premier temps, il est impératif de s'assurer que les valeurs sont bien rangées dans l'ordre croissant. Ici, c'est bien le cas.
L'effectif total est qui est pair, donc la médiane est la moyenne des valeurs centrales.
Nous partageons cette série statistique en deux groupes de même effectif. Comme l'effectif total est 6, nous pouvons créer deux groupes de 3 valeurs.
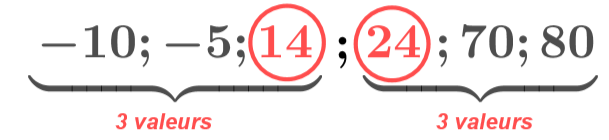
Par convention, on prend exactement la moyenne des deux valeurs centrales : entre et , c'est-à-dire :
Donc la médiane de la série statistique est
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.