Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : 4ème partie - Exercice 2
12 min
25
On lance la roue de loterie suivante : 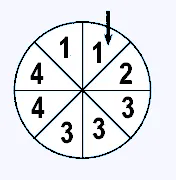

Question 1
Quelle est la probabilité des évènements suivants :
" La roue s'arrête sur le nombre est ."
Correction
En observant notre roue, on constate qu'il y a issues qui réalisent l'évènement : .
La roue est composée de issues possibles, donc il y a 8 possibilités au total.
On peut donc conclure, que la probabilité que la roue s'arrête sur le nombre est :
- La probabilité d'un évènement A, est notée P(A) et cette probabilité est définie par le quotient suivant :
On peut donc conclure, que la probabilité que la roue s'arrête sur le nombre est :
Question 2
" La roue s'arrête sur un multiple de ."
Correction
En observant notre roue, on constate qu'il y a issues qui réalisent l'évènement : .
La roue est composée de issues possibles, donc il y a 8 possibilités au total.
On peut donc conclure, que la probabilité que la roue s'arrête sur un multiple de est :
- La probabilité d'un évènement A, est notée P(A) et cette probabilité est définie par le quotient suivant :
On peut donc conclure, que la probabilité que la roue s'arrête sur un multiple de est :
Question 3
" La roue s'arrête sur un diviseur de ."
Correction
Ici il nous faut déterminer les diviseurs de :
On calcule la racine carré de , on obtient :
On divise par tous les nombres entiers allant de à sa racine carrée, c'est-à-dire
donc et sont des diviseurs de
donc et sont des diviseurs de
On peut donc conclure que tous les diviseurs de , sont :
En observant notre roue, on constate qu'il y a issues qui réalisent l'évènement :
On peut donc conclure, que la probabilité que la roue s'arrête sur un diviseur de est :
On calcule la racine carré de , on obtient :
On divise par tous les nombres entiers allant de à sa racine carrée, c'est-à-dire
donc et sont des diviseurs de
donc et sont des diviseurs de
On peut donc conclure que tous les diviseurs de , sont :
En observant notre roue, on constate qu'il y a issues qui réalisent l'évènement :
On peut donc conclure, que la probabilité que la roue s'arrête sur un diviseur de est :
Question 4
" La roue s'arrête sur un nombre impair."
Correction
En observant notre roue, les nombres impairs sont : , donc il y a issues qui réalisent l'évènement .
La roue est composée de issues possibles, donc il y a 8 possibilités au total.
On a 5 nombres impairs, on peut donc conclure, que la probabilité que la roue s'arrête sur un nombre impair est :
- La probabilité d'un évènement A, est notée P(A) et cette probabilité est définie par le quotient suivant :
On a 5 nombres impairs, on peut donc conclure, que la probabilité que la roue s'arrête sur un nombre impair est :
Question 5
" La roue s'arrête sur un nombre premier"
Correction
- La probabilité d'un évènement A, est notée P(A) et cette probabilité est définie par le quotient suivant :
On a 4 nombres premiers, on peut donc conclure, que la probabilité que la roue s'arrête sur un nombre premier est :
Question 6
" La roue s'arrête sur un nombre supérieur à ."
Correction
En observant notre roue, on constate qu'il n'y a aucun nombre supérieur à , donc il y a issues qui réalisent l'évènement .
La roue est composée de issues possibles, donc il y a 8 possibilités au total.
On peut donc conclure, que la probabilité que la roue s'arrête sur un nombre supérieur à est :
La roue est composée de issues possibles, donc il y a 8 possibilités au total.
On peut donc conclure, que la probabilité que la roue s'arrête sur un nombre supérieur à est :
Question 7
" La roue s'arrête sur un diviseur de ."
Correction
Ici il nous faut déterminer les diviseurs de :
On calcule la racine carrée de , on obtient :
On divise par tous les nombres entiers allant de à sa racine carrée, c'est-à-dire
donc et sont des diviseurs de
donc et sont des diviseurs de
donc et sont des diviseurs de
On peut donc conclure que tous les diviseurs de , sont :
En observant notre roue, on constate que toutes les issues réalisent l'évènement .
On peut donc conclure, que la probabilité que la roue s'arrête sur un diviseur de est : . (C'est un évènement certain).
On calcule la racine carrée de , on obtient :
On divise par tous les nombres entiers allant de à sa racine carrée, c'est-à-dire
donc et sont des diviseurs de
donc et sont des diviseurs de
donc et sont des diviseurs de
On peut donc conclure que tous les diviseurs de , sont :
En observant notre roue, on constate que toutes les issues réalisent l'évènement .
On peut donc conclure, que la probabilité que la roue s'arrête sur un diviseur de est : . (C'est un évènement certain).
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.