Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Tchat avec un prof

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Exercices types : 3ème partie - Exercice 1

15 min
25
Question 1
Un joueur lance une roue représentée ci-dessous qui possède huit secteurs colorés.

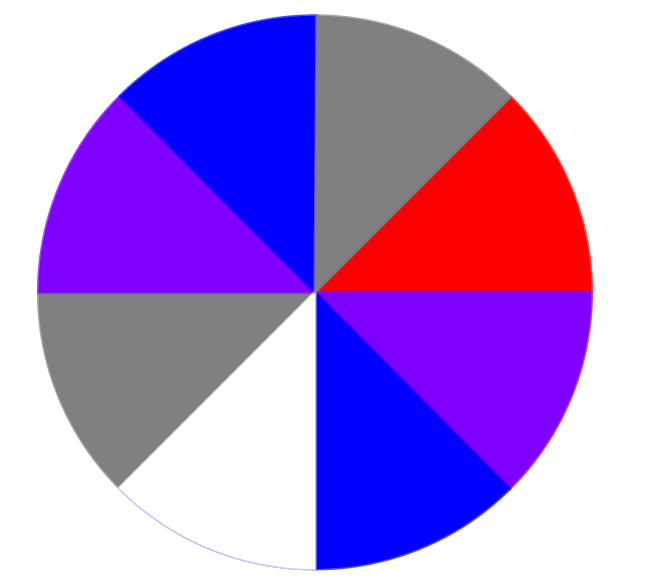
Quelle est la probabilité que la roue s'arrête sur le rouge ?

Correction
  • La probabilité d'un évènement A est notée P(A), cette probabilité est définie par le quotient suivant :                                                                \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P(A)=nombre  de  cas  favorables    aˋ  Anombre de  cas  possibles\color{red}P(A)=\frac{\small\text{nombre\;de\;cas\;favorables\;\;à\;A}}{\small\text{nombre\,de\;cas\;possibles}}
La roue est composée de 88 secteurs colorés, donc il y a 8 possibilités au total.
On a un secteur coloré en rouge, on peut donc conclure, que la probabilité que la roue s'arrête sur le rouge est de : 18\color{blue}\boxed{\frac{1}{8}}
Question 2

Quelle est la probabilité que la roue s'arrête sur le gris ?

Correction
  • La probabilité d'un évènement A est notée P(A), cette probabilité est définie par le quotient suivant :                                                                :\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P(A)=nombre  de  cas  favorables    aˋ  Anombre de  cas  possibles\color{red}P(A)=\frac{\small\text{nombre\;de\;cas\;favorables\;\;à\;A}}{\small\text{nombre\,de\;cas\;possibles}}
La roue est composée de 88 secteurs colorés, donc il y a 8 possibilités au total.
On a 2 secteurs colorés en gris, on peut donc conclure, que la probabilité que la roue s'arrête sur le gris est de : 28=14\color{blue}\boxed{\frac{2}{8}=\frac{1}{4}}
Question 3
Le joueur a fait tourner la roue à cinq reprises, et a obtenu un secteur blanc à chaque fois.

Au 6eˋme6^{ème} lancer, peut-on affirmer qu'il aura plus de chance de tomber sur un secteur blanc que sur un secteur bleu.

Correction
La roue est composée de 22 secteurs gris, 22 secteurs violets, 22 secteurs bleus, 11 secteur blanc et 11 secteur rouge.
  • La probabilité d'un évènement A est notée P(A), cette probabilité est définie par le quotient suivant :                                                                :\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P(A)=nombre  de  cas  favorables    aˋ  Anombre de  cas  possibles\color{red}P(A)=\frac{\small\text{nombre\;de\;cas\;favorables\;\;à\;A}}{\small\text{nombre\,de\;cas\;possibles}}
La roue est composée de 88 secteurs colorés, donc il y a 8 possibilités au total.
On a 1 secteur coloré en blanc.
Donc au 6eˋme6^{ème} lancer, la probabilité de tomber sur un secteur blanc sera de : 18\color{blue}\boxed{\frac{1}{8}}.
On a 2 secteurs colorés en bleus.
La probabilité de tomber sur un secteur bleu sera de : 28=14\color{blue}\boxed{\frac{2}{8}=\frac{1}{4}}.
Or 28>18\frac{2}{8}>\frac{1}{8}
Alors à son 6eˋme6^{ème} lancer, il aura plus de chance de tomber sur un secteur bleu que sur un secteur blanc.
L'affirmation est donc fausse.

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.