Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Sujet 2 - Exercice 1
8 min
15
Question 1
Le départ en croisière choisi par Julien a lieu le juillet (entre et ).
Le graphique ci-dessous décrit les variations de la hauteur de la mer dans le port de Fort de France selon l’heure de la matinée (entre et ) du juillet.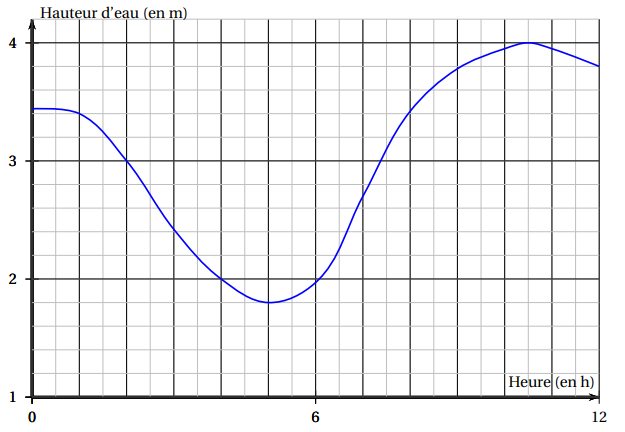
On nomme la fonction définie par cette courbe.
Le graphique ci-dessous décrit les variations de la hauteur de la mer dans le port de Fort de France selon l’heure de la matinée (entre et ) du juillet.

On nomme la fonction définie par cette courbe.
Le voilier ne peut pas sortir du port que si la hauteur d’eau dépasse mètres. Quelles sont les tranches horaires de départs possibles pour ce voilier
Correction
À l'aide de notre graphique ci-dessous, on constate que le voilier peut quitter le port entre et ou entre et .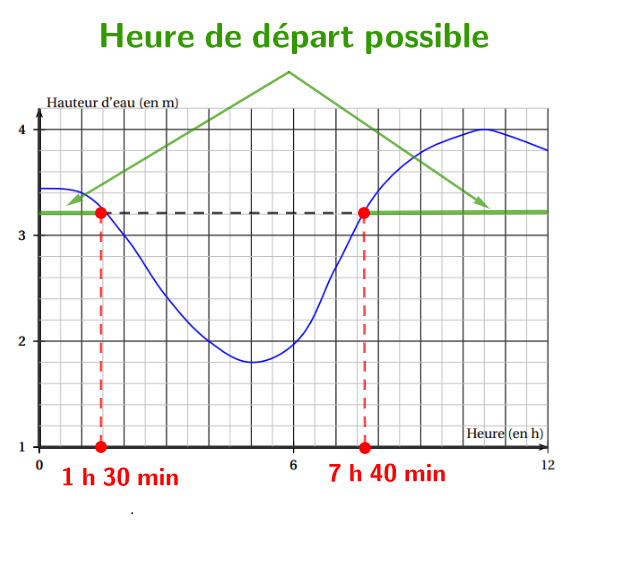

Question 2
Finalement, Julien, le skipper du voilier, décide de partir lorsque la hauteur d’eau est maximale. À quelle heure Julien va-t-il partir ?
Correction
La hauteur d'eau est situé au maximum de la courbe (là où elle est la plus haute).
À l'aide du graphique ci-dessous, on peut en déduire que Julien partira à .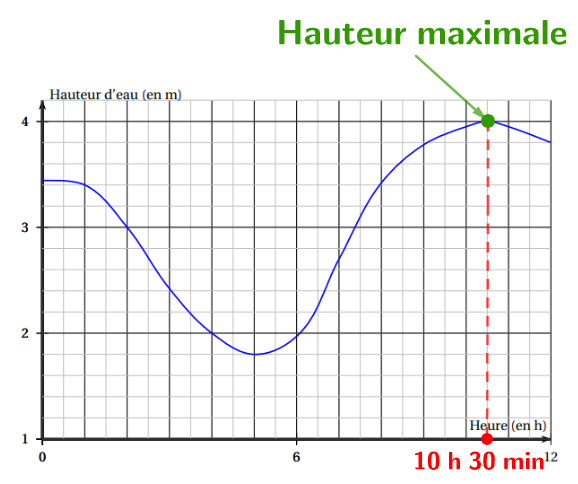
À l'aide du graphique ci-dessous, on peut en déduire que Julien partira à .

Question 3
Donner la (ou les) image(s) de par la fonction Interpréter le résultat.
Correction
Ici, on souhaite déterminer l'image de par la fonction , c'est-à-dire . Pour cela :
On repère le point d'abscisse , et ensuite, on rejoint la courbe verticalement.
Ensuite, en partant du point de la courbe, on rejoint l'axe des ordonnées. (En ce point se trouve la valeur recherchée.)
À l'aide du graphique, on peut en conclure que l'image de par la fonction est . On peut l'écrire également :
On peut donc conclure qu'à la hauteur d'eau sera de .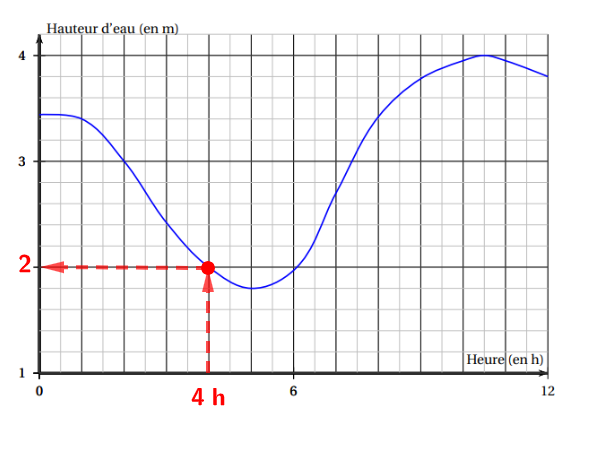
On repère le point d'abscisse , et ensuite, on rejoint la courbe verticalement.
Ensuite, en partant du point de la courbe, on rejoint l'axe des ordonnées. (En ce point se trouve la valeur recherchée.)
À l'aide du graphique, on peut en conclure que l'image de par la fonction est . On peut l'écrire également :
On peut donc conclure qu'à la hauteur d'eau sera de .

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.