Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Tchat avec un prof

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Exercices types homothétie: 2ème partie - Exercice 1

7 min
10
Question 1
On considère la figure suivante :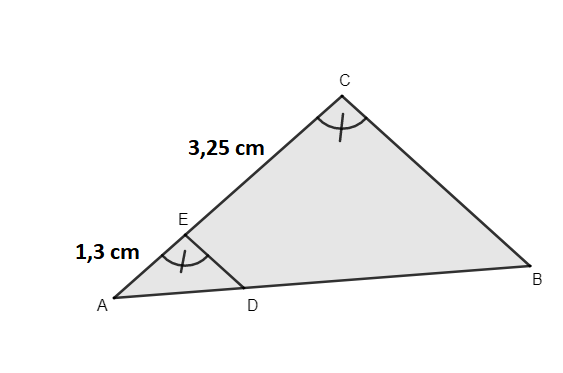

Montrer que les triangles ACBACB et AEDAED sont semblables.

Correction
Si deux triangles ont seulement deux paires d'angles de même mesure alors, ils sont semblables.
À l'aide de la figure ci-dessus, on constate que :
AED^=ACB^\widehat{AED}=\widehat{ACB}
On peut donc déjà en déduire que les deux triangles ont une paire d'angles de même mesure.
Dans un second temps, on sait que les triangles ACBACB et AEDAED ont le sommet AA en commun, par conséquent :
EAD^=CAB^\widehat{EAD}=\widehat{CAB}
On peut donc conclure que les triangles ACBACB et AEDAED ont deux paires d'angles de la même mesure ils sont donc semblables.
Question 2
Le triangle ABCABC est l'image du triangle ADEADE par une homothétie de centre AA et de rapport kk.

Quelle est la valeur de kk.

Correction
  • Définition : Pour déterminer le coefficient kk, il faut calculer le rapport des côtés homologues
k=ACAE=4,551,3  k=\frac{AC}{AE}=\frac{4,55}{1,3}\; Avec AC=AE+EC=1,3+3,25=4,55  cmAC=AE+EC=1,3+3,25=4,55\;cm
k=3,5\color{blue}\boxed{k=3,5}
Question 3

Si AD=2,5  cmAD=2,5\;cm, Quelle est la longueur de [AB]?[AB]?

Correction
  • Dans le cas d'un agrandissement de rapport kk, on a :
  • La longueur d'un segment obtenu après l'agrandissement =k  ×\color{red}=k\;\times longueur du segment initiale.
Ici, on a un rapport k=3,5k=3,5, avec AD=2,5  cm.AD=2,5\;cm. Par conséquent, on a :
AB=k×ADAB=k\times{AD}
AB=3,5×2,5AB=3,5\times{2,5}
AB=8,75  cm\color{blue}\boxed{AB=8,75\;cm}
On peut donc conclure que le segment [AB]\color{blue}[AB] mesure 8,75  cm8,75\;cm.

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.