Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types homothétie : 1ère partie - Exercice 1
12 min
30
Question 1
Avec un logiciel de géométrie dynamique, on a construit la figure . En appliquant à la figure des homothéties de centre et de rapports différents, on a ensuite obtenu les autres figures.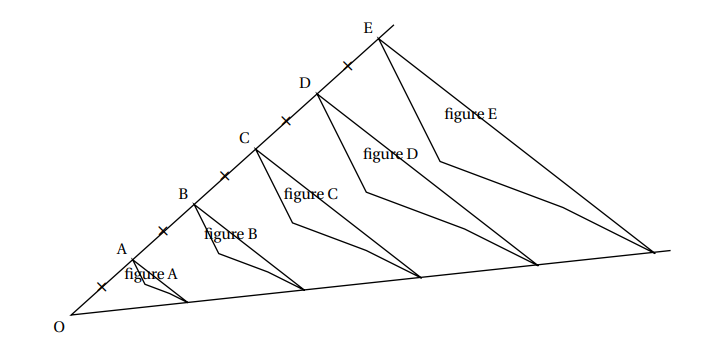

Quel est le rapport de l’homothétie de centre qui permet d’obtenir la figure à partir de la figure ? Aucune justification n’est attendue.
Correction
Sur le schéma ci-dessus, on constate que donc,
Par conséquent, on peut conclure que le rapport de l’homothétie de centre qui permet d’obtenir la figure à partir de la figure est
Par conséquent, on peut conclure que le rapport de l’homothétie de centre qui permet d’obtenir la figure à partir de la figure est
Question 2
On applique l’homothétie de centre et de rapport à la figure . Quelle figure obtient-on ?
Aucune justification n’est attendue.
Aucune justification n’est attendue.
Correction
Sur le schéma ci-dessus, on constate que
On en déduit donc que le segment est découpé en parts égales.
Donc si on applique l’homothétie de centre et de rapport à la figure , alors le point se transforme en le point .
En effet :
Donc on peut donc conclure que la figure se transforme en la figure .
On en déduit donc que le segment est découpé en parts égales.
Donc si on applique l’homothétie de centre et de rapport à la figure , alors le point se transforme en le point .
En effet :
Donc on peut donc conclure que la figure se transforme en la figure .
Question 3
Quelle figure a une aire quatre fois plus grande que celle de la figure ?
Correction
- Lorsque les dimensions d’une figure sont multipliées par un nombre positif , nous obtenons une
nouvelle figure dont l’aire est multipliée par
On peut donc en déduire que les longueurs ont été multipliées par , en effet
Or, on sait que donc
Donc le rapport d’homothétie permettant de passer de la figure à la figure est :
Donc on peut donc conclure que la figure a une aire quatre fois plus grande que la figure .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.