Qui aura 20 en maths ?

💯 Le grand concours 100% Terminale revient le 31 mai 2026 en ligne !Découvrir  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Sujet 3 - Exercice 1

15 min
25
Question 1

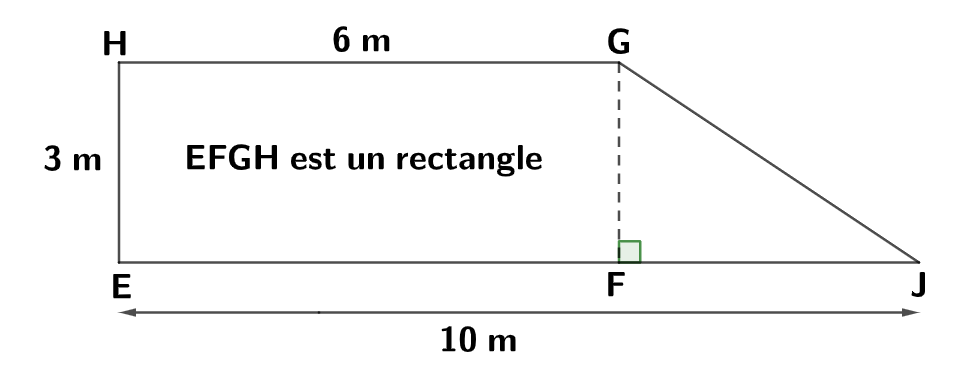
Montrer que FJ=4  m.FJ = 4\;m.

Correction
EFGHEFGH est un rectangle.
Or un triangle à ses côtés opposés de la même longueur, donc HG=EF=6  mHG=EF=6\;m.
Or FJ=EJ−EFFJ = EJ - EF avec EJ=10  m.EJ=10\;m.
FJ=10−6=4  m.\boxed{FJ=10−6=4\;m}.
Question 2

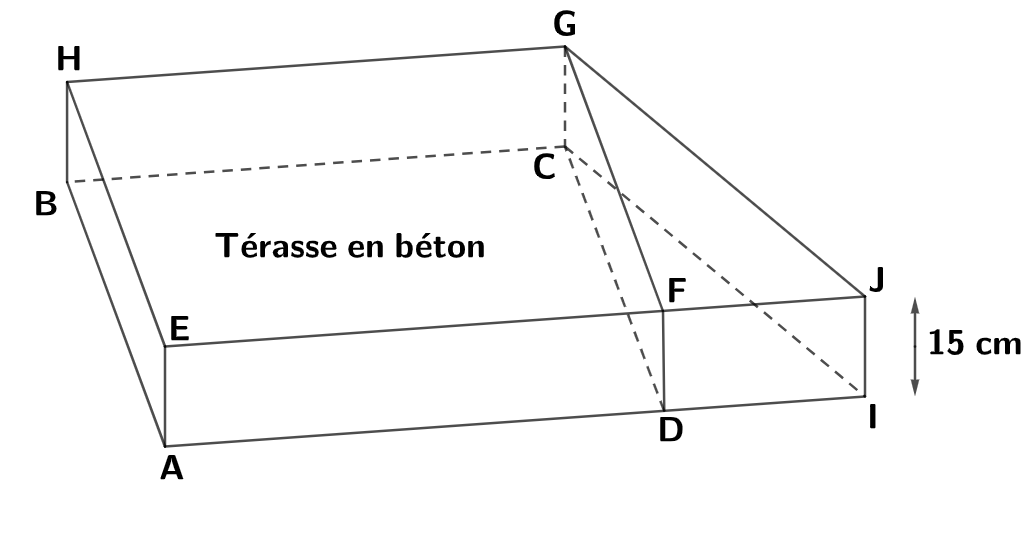
Afin de pouvoir couler le béton, M. et Mme Martin doivent délimiter la terrasse en installant des planches tout autour. Quelle longueur de planches doivent-ils acheter au minimum ?

Correction
Ici, il nous faut calculer le périmètre de la terrasse.
Peˊrimeˋtrede  la  terasse=EF+FJ+JG+GH+HEPérimètre_{de\;la\;terasse}=EF + FJ + JG + GH + HE
Nous connaissons toutes les longueurs, hormis JG.JG.
Comme le triangle GFJGFJ est rectangle en FF avec GF=3GF= 3 m et FJ=4FJ = 4 m.

On peut appliquer le théorème de Pythagore :

JG2=GF2+FJ2JG^{2} =GF^{2} +FJ^{2}

donc :
JG2=32+42JG^{2} =3^{2} +4^{2}
JG2=9+16JG^{2} =9+16
JG2=25JG^{2} =25

Nous allons utiliser la racine carrée pour déterminer la mesure de JGJG.

D'où :
JG=25JG=\sqrt{25}

Ainsi :
JG=5JG=5 m

La mesure de JGJG est donc de 55 m.
Peˊrimeˋtrede  la  terasse=EF+FJ+JG+GH+HEPérimètre_{de\;la\;terasse}=EF + FJ + JG + GH + HE
Peˊrimeˋtrede  la  terasse=6+4+5+6+3Périmètre_{de\;la\;terasse}=6+4+5+6+3
Peˊrimeˋtrede  la  terasse=24Périmètre_{de\;la\;terasse}=24 m
Ils devront donc acheter 2424 m de planches.
Question 3
M. et Mme Martin souhaitent réaliser 4  m34\;m^3 de béton.

Montrer que le volume de la terrasse est bien inférieur à 4  m3.4\;m^3.
.

Correction
Ici, on doit calculer le volume de la terrasse (qui est un prisme).
volumeprisme=Aire  de  la  base×hauteurvolume_{prisme}=Aire\;de\;la\;base\times{hauteur}
La base de la terrasse est composée d'un triangle et d'un rectangle.
Aire  du  rectangle=longueur×largeur=3×6=18  m2Aire\;du\;rectangle=longueur\times{largeur}=3\times6=18\;m^2
Aire  du  triangle=base×hauteur2=FJ×GF2Aire\;du\;triangle=\frac{base\times{hauteur}}{2}=\frac{FJ\times{GF}}{2}
Aire  du  triangle=4×32=6m2Aire\;du\;triangle=\frac{4\times{3}}{2}=6m^2
L'aire de la base du prisme est égale à la somme de l'aire du rectangle et de l'aire du triangle soit : 18+6=24  m2\color{blue}18+6=24\;m^2.
La hauteur du prisme est de 15  cm15\;cm soit 0,150,15 m.
volumeprisme=Aire  de  la  base×hauteur=24×0,15volume_{prisme}=Aire\;de\;la\;base\times{hauteur}=24\times0,15
volumeprisme=3,6  m3\boxed{volume_{prisme}=3,6\;m^3}
3,6<4,3,6<4, Le volume de la térasse est donc bien inférieur à 4  m34\;m^3.
Question 4

Sachant que pour faire 1  m31\;m^3 de béton, il faut 250  kg250\;kg de ciment, quelle masse de ciment ((en kg)kg) doivent-ils acheter pour réaliser 4  m34\;m^3 de béton ??

Correction
Ici, on sait que pour 1  m31\;m^3 de béton, on a besoin de 250250 kg de ciment.
Donc pour réaliser 4  m34\;m^3 de béton, ils auront besoin de : 4×250=1  000  kg4\times250=1\;000\;kg de ciments.
Question 5
Pour faire du béton, on ajoute de l’eau à un mélange de ciment, de gravier et de sable.

Dans ce mélange, les masses de ciment −- gravier −- sable sont dans le ratio 2:7:5.2 : 7 : 5.
Déterminer ((en kg),kg), la masse de gravier et la masse de sable nécessaires pour réaliser les 4m34m^3 de béton.

Correction
Dans ce mélange, les masses de ciment − - gravier− - sable sont dans le ratio 2:7:52 : 7 : 5.
Par proportionalité on peut aussi dire que le ratio 2:7:52 : 7 : 5 peut sécrire 1:3,5:2,51:3,5:2,5. Ici, on divise chaque valeur par 22.
C'est-à-dire :
  • Que la masse de ciment représente 1  000  kg1\;000\;kg.
    Dans le mélange, il y aura 1  000  kg\color{blue}1\;000\;kg de ciment.
  • La proportion de gravier est 3,53,5 fois plus importante soit : 3,5×  1  000=3  500  kg3,5\times\;1\;000=3\;500\;kg
    Dans le mélange, il y aura 3  500  kg\color{blue}3\;500\;kg de gravier.
  • La proportion de sable est 2,52,5 fois plus importante soit : 2,5×  1  000=2  500  kg2,5\times\;1\;000=2\;500\;kg
    Dans le mélange, il y aura 2  500  kg\color{blue}2\;500\;kg de sable.
    • Question 6
    M. et Mme Martin souhaitent peindre la surface supérieure de leur terrasse.

    À l’aide des documents 1,21,2 et 3,3, déterminer le type et le nombre de pots nécessaires pour effectuer ces travaux avec un coût minimum.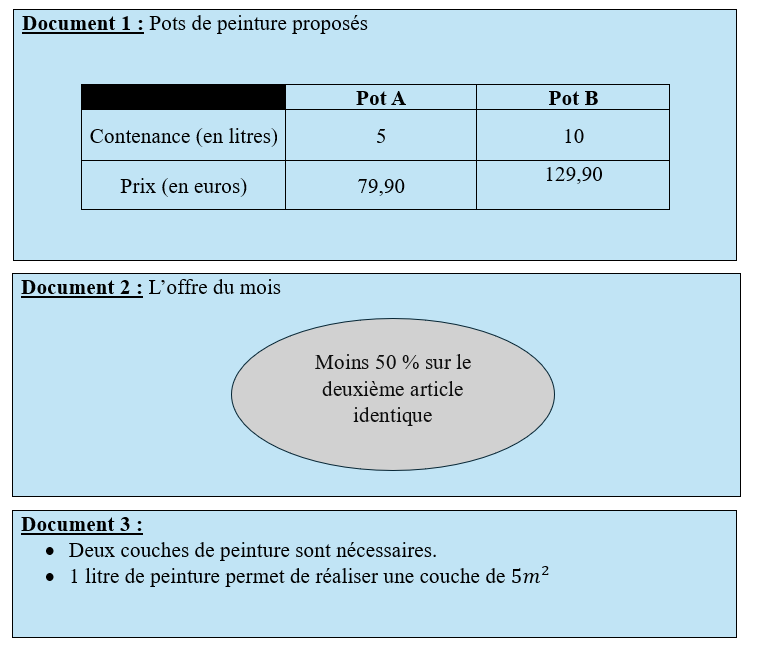

    Correction
    À la question 3.a3.a, on sait que la surface de la terrasse est de 24  m324\;m^3.
    À l'aide du document 33 ci-dessus, on précise que l'on a besoin de mettre 22 couches de peintures.
    Au total, cela correspond à une surface à peindre de 24×2=48  m224\times2=48\;m^2.
    On sait que 11 litre de peinture permet de réaliser une couche de 5m2.5m^2.

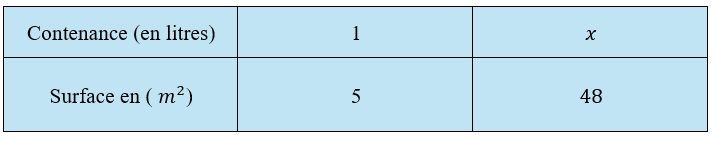
    Ici, on a une situation de proportionnalité, x=1×485=9,61x=\frac{1\times48}{5}=9,61 litres.
    On aura donc besoin de 1010 litres de peinture.
    D'après le document 11 :
  • On sait qu'en utilisant le pot BB d'une contenance de 1010 litres, le prix à payer sera de 129,90129,90 euros.
    Concernant le pot AA, il nous faudra 22 pots dont le deuxième sera à 50  %50\;\% d'après le document 22.
  • Le prix à payer sera donc de 79,90+79,902=119,8579,90+\frac{79,90}{2}=119,85 euros.
    Il sera donc plus avantageux d'acheter deux pots AA pour avoir un coût minimum.

    • Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.