Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →

Sujet 3 - Exercice 1

20 min

Question 1

On considère la fonction

g

représentée dans le repère ci-dessous.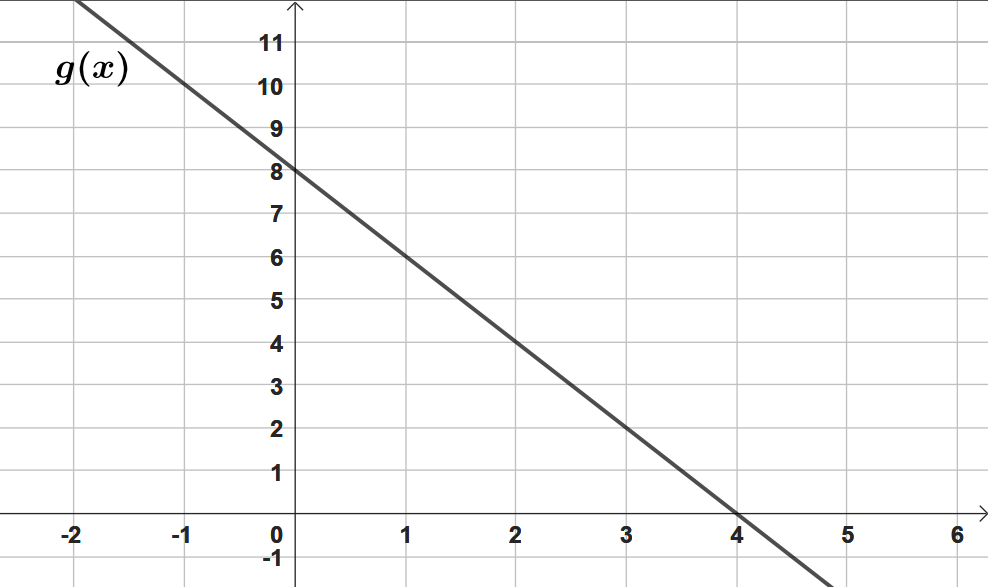

Donner l’antécédent de $4$ par la fonction $g$ .

Correction

Ici, on souhaite déterminer l'antécédent de

4

par la fonction

g

, c'est-à-dire trouver la valeur de

x

tel que

g(x)=4

. Pour cela :

\bullet

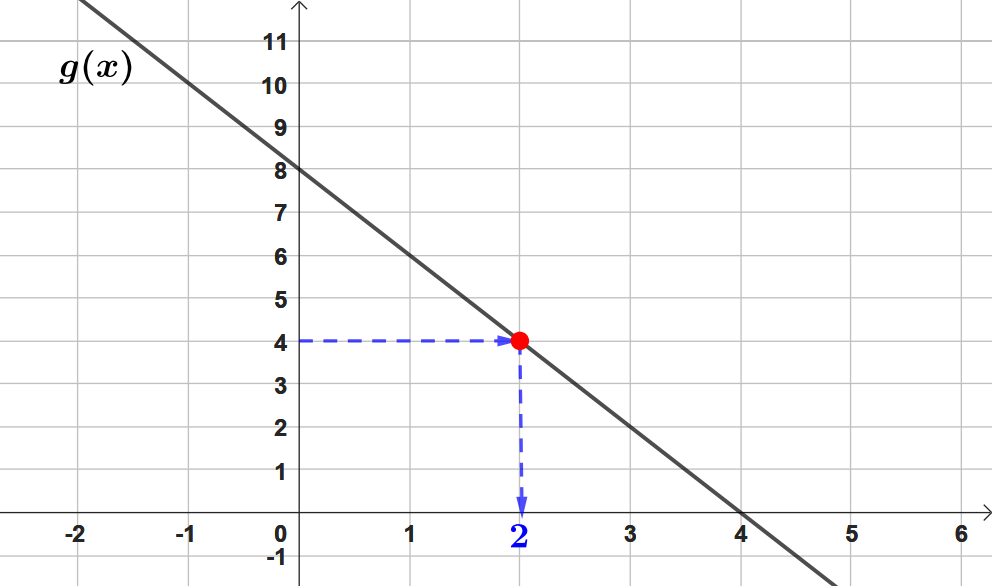
On repère le point d'ordonnée $4$ , et ensuite, on rejoint la courbe horizontalement. (Cela revient à tracer la droite d'équation $y=4$ .)
$\bullet$ Ensuite, au(x) point(s) d'intersection de la droite d'équation $y=4$ et de la courbe, on rejoint l'axe des abscisses. (En ce point se trouve là où les valeur(s) recherchée(s).)
À l'aide du graphique, on peut en conclure que l'antécédent de $\color{blue}4$ par la fonction $\color{blue}g$ est $\color{blue}2$ .

Question 2

Compléter le tableau de valeurs de la fonction $g$ ci-dessous.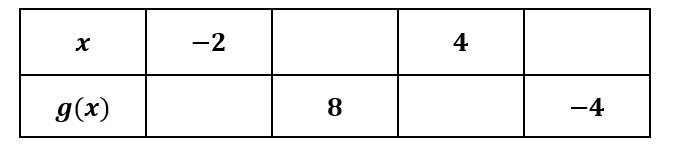

Correction

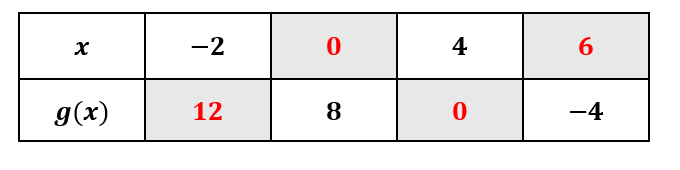
Question 3

La fonction

f

est donnée par

f (x) = 2x.

Quelle est l’image de $−2$ par la fonction $f$ ?

Correction

f

est la fonction linéaire

f\left(x\right)=2x

.
Pour déterminer l'image de

-2

par

f

, il nous suffit de remplacer $x$ par $-2$ .
Il vient alors que :

f\left(-2\right)=2\times (-2)

f\left(-2\right)=-4

L'image de $-2$ par $f$ vaut $-4$ .

Question 4

Calculer $f(3)$ .

Correction

f

est la fonction linéaire

f\left(x\right)=2x

.
Pour déterminer l'image de

3

par

f

, il nous suffit de remplacer $x$ par $3$ .
Il vient alors que :

f\left(3\right)=2\times 3

f\left(3\right)=6

L'image de $3$ par $f$ vaut $6$ .

Question 5

Tracer la représentation graphique de la fonction $f$ .

Correction

Pour tracer une droite, on a besoin de deux points.

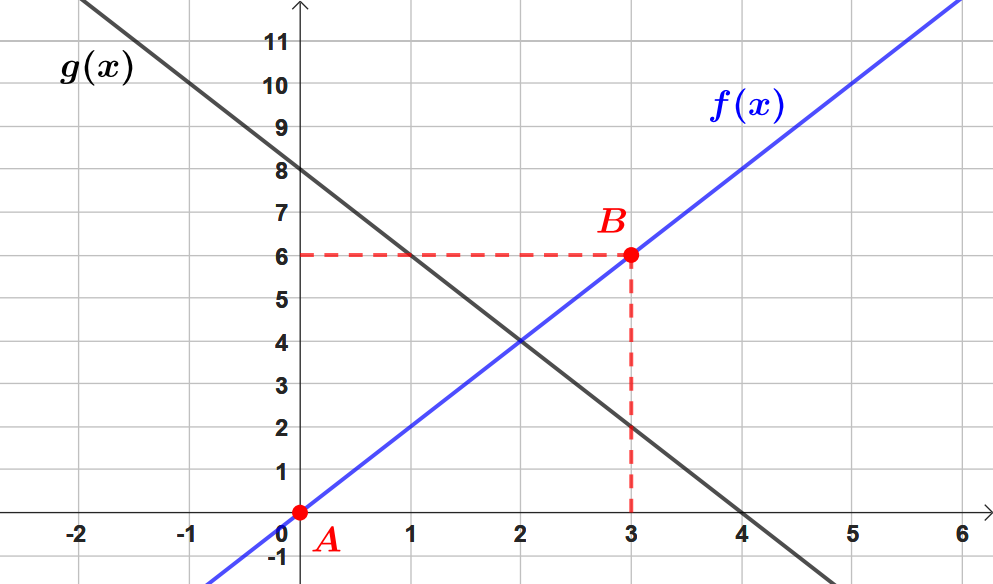
La représentation graphique d'une fonction linéaire est une droite qui passe par l'origine du repère

On connait déjà les coordonnées d'un premier point, (l'origine du repère).
Ensuite, il faut de déterminer un autre point pour pouvoir tracer la droite.
Pour cela, on calcule l'image d'un nombre quelconque, prenons ici par exemple l'image de $3$ .
À l'aide de la question précédente, on sait que l'image de 3 par $f$ vaut $6$ . Ici, on a donc les coordonnées du deuxième point $B\;(3;6).$

Question 6

Déterminer graphiquement l’abscisse du point d’intersection $S$ des deux représentations graphiques.
Faire apparaître en pointillés la lecture sur le graphique.

Correction

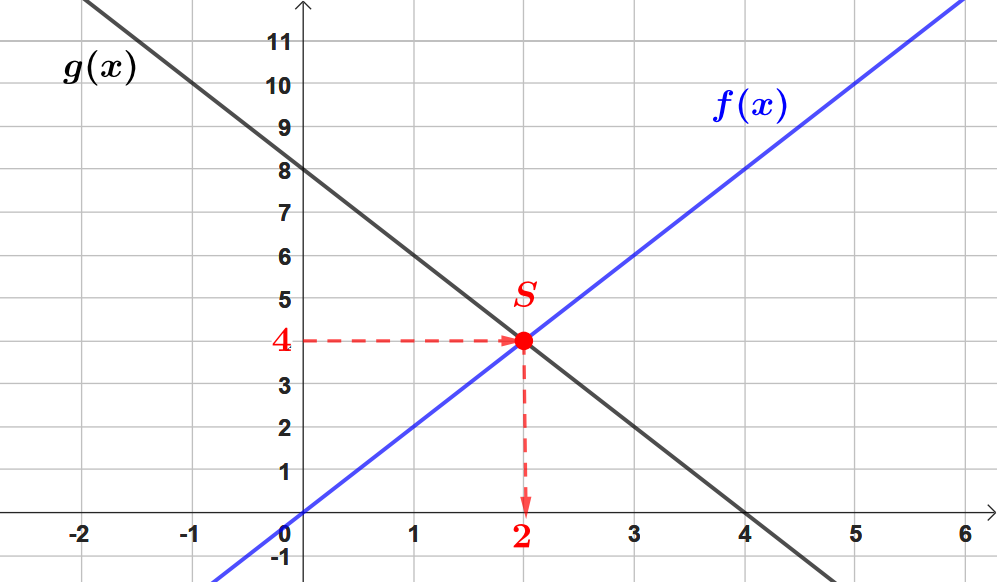
Graphiquement, on peut conclure que l'abscisse du point d'intersection des droites, est $\color{blue}x=2$ .

Question 7

L’expression de la fonction

g

est

g (x) = −2x +8.

Résoudre l’équation $2x = −2x +8.$

Correction

2x = −2x +8.

On doit dans un premier temps rassembler les termes en $x$ dans le membre de gauche.

2x{\color{blue}+2x}=-2x+8{\color{blue}+2x}\;

On additionne ${\color{blue}2x}$ à chaque membre .

4x=8

\frac{4x}{\color{blue}4}=\frac{8}{\color{blue}4}\;

On divise chaque membre par le nombre devant le $x$ qui ici vaut ${\color{blue}4}$ .
Ainsi :

x=2

L'ensemble des solutions est

S=\left\{2\right\}

Sujet 3 - Exercice 1

Donner l’antécédent de 444 par la fonction ggg.

Compléter le tableau de valeurs de la fonction ggg ci-dessous.

Quelle est l’image de −2−2−2 par la fonction fff ?

Calculer f(3)f(3)f(3).

Tracer la représentation graphique de la fonction fff.

Déterminer graphiquement l’abscisse du point d’intersection SSS des deux représentations graphiques.Faire apparaître en pointillés la lecture sur le graphique.

Résoudre l’équation 2x=−2x+8.2x = −2x +8.2x=−2x+8.

Donner l’antécédent de $4$ par la fonction $g$ .

Compléter le tableau de valeurs de la fonction $g$ ci-dessous.

Quelle est l’image de $−2$ par la fonction $f$ ?

Calculer $f(3)$ .

Tracer la représentation graphique de la fonction $f$ .

Déterminer graphiquement l’abscisse du point d’intersection $S$ des deux représentations graphiques.
Faire apparaître en pointillés la lecture sur le graphique.

Résoudre l’équation $2x = −2x +8.$