Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Déterminer une image ou un antécédent à partir d'une droite - Exercice 4
7 min
10
COMPETENCES : Savoir lire et interpréter différentes valeurs graphiquement.
Question 1
Ici est la représentation graphique d'une fonction linéaire .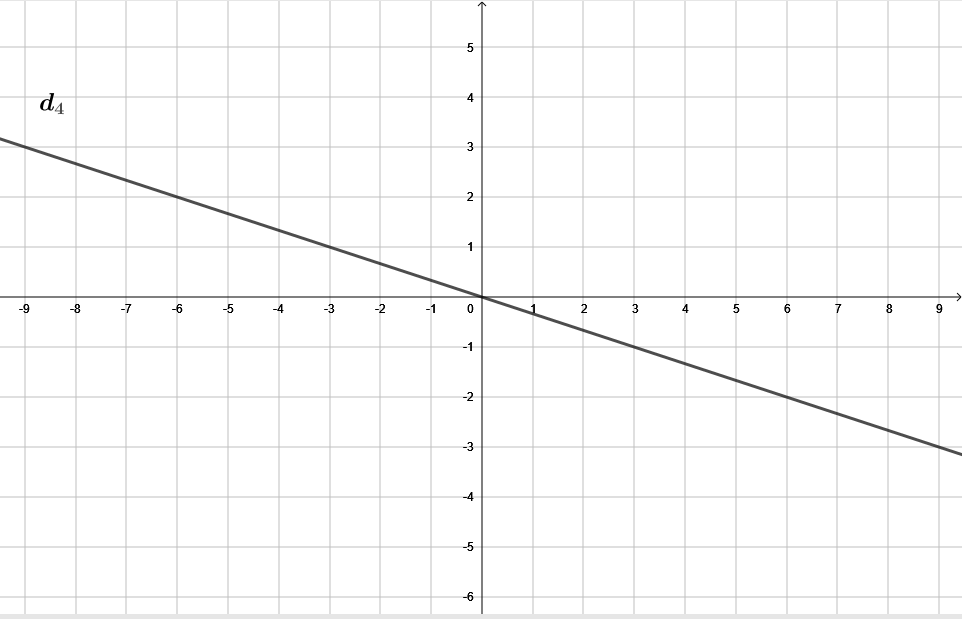

Quelle est l'image de par la fonction ?
Correction
Ici, on souhaite déterminer l'image de par la fonction , c'est-à-dire . Pour cela :
On repère le point d'abscisse , et ensuite, on rejoint la courbe verticalement.
Ensuite, en partant du point de la courbe, on rejoint l'axe des ordonnées. (En ce point se trouve la valeur recherchée.)
À l'aide du graphique, on peut en conclure que l'image de par la fonction f est . On peut l'écrire également :
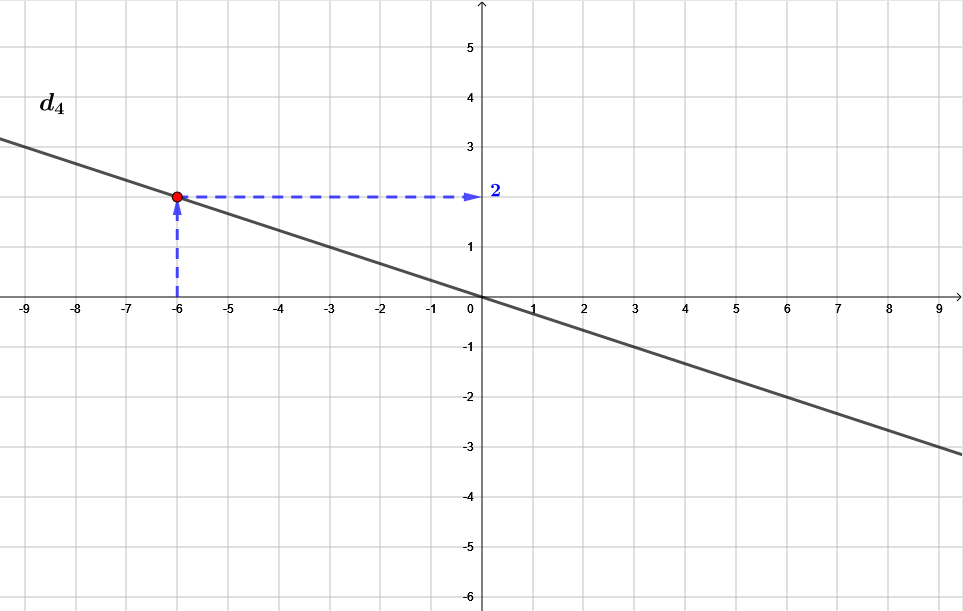
On repère le point d'abscisse , et ensuite, on rejoint la courbe verticalement.
Ensuite, en partant du point de la courbe, on rejoint l'axe des ordonnées. (En ce point se trouve la valeur recherchée.)
À l'aide du graphique, on peut en conclure que l'image de par la fonction f est . On peut l'écrire également :

Question 2
Quelle est l'image de par la fonction ?
Correction
Ici, on souhaite déterminer l'image de par la fonction , c'est-à-dire . Pour cela :
On repère le point d'abscisse , et ensuite, on rejoint la courbe verticalement.
Ensuite, en partant du point de la courbe, on rejoint l'axe des ordonnées. (En ce point se trouve la valeur recherchée.)
À l'aide du graphique, on peut en conclure que l'image de par la fonction f est . On peut l'écrire également :
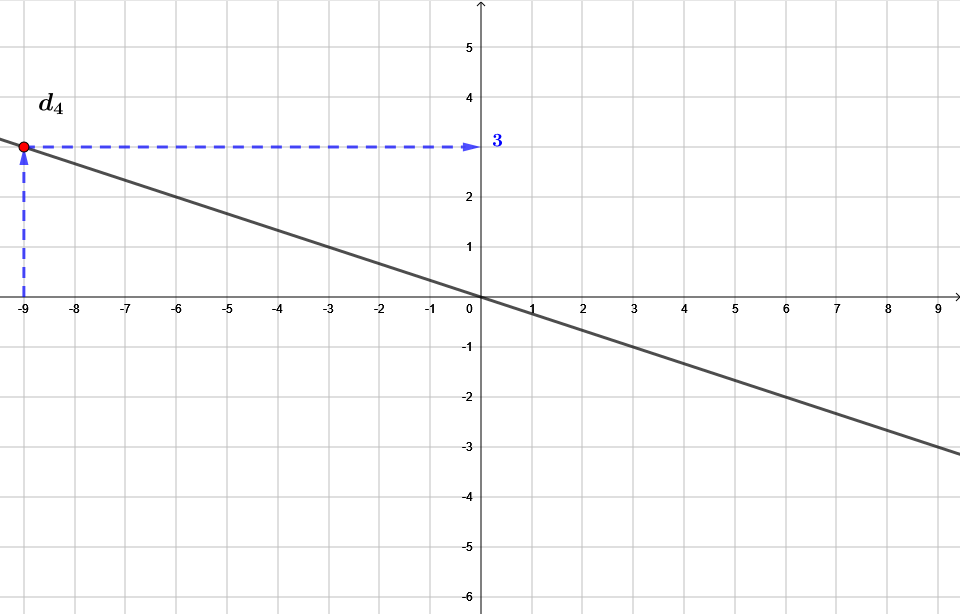
On repère le point d'abscisse , et ensuite, on rejoint la courbe verticalement.
Ensuite, en partant du point de la courbe, on rejoint l'axe des ordonnées. (En ce point se trouve la valeur recherchée.)
À l'aide du graphique, on peut en conclure que l'image de par la fonction f est . On peut l'écrire également :

Question 3
Déterminer graphiquement l'antécédent de par .
Correction
Ici, on souhaite déterminer l'antécédent de par la fonction , c'est-à-dire trouver la valeur de tel que . Pour cela :
On repère le point d'ordonnée , et ensuite, on rejoint la courbe horizontalement. (Cela revient à tracer la droite d'équation .)
Ensuite, au(x) point(s) d'intersection de la droite d'équation et de la courbe, on rejoint l'axe des abscisses. (En ce point se trouve là où les valeur(s) recherchée(s).)
A l'aide du graphique, on peut en conclure que l'antécédent de par la fonction est .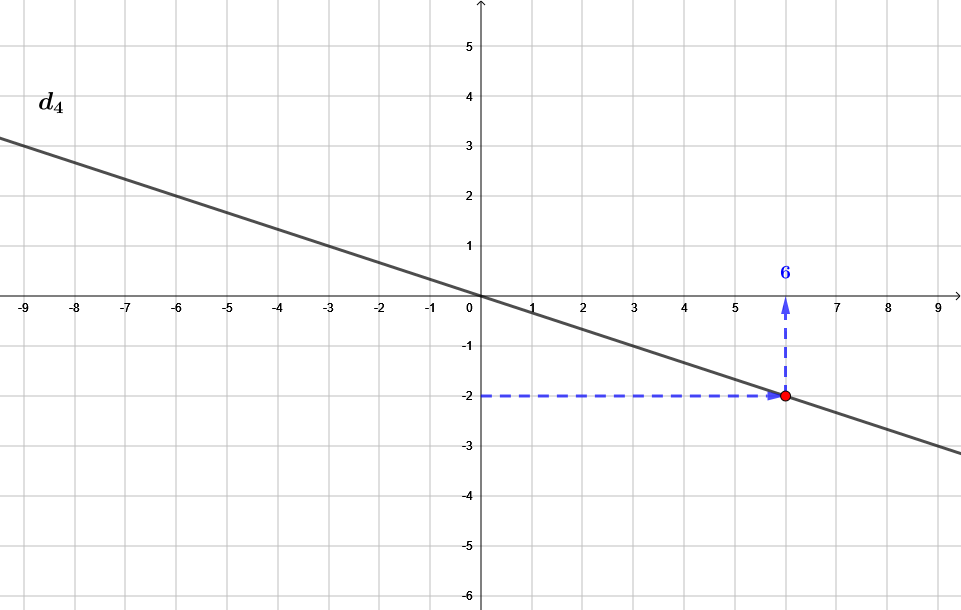
On repère le point d'ordonnée , et ensuite, on rejoint la courbe horizontalement. (Cela revient à tracer la droite d'équation .)
Ensuite, au(x) point(s) d'intersection de la droite d'équation et de la courbe, on rejoint l'axe des abscisses. (En ce point se trouve là où les valeur(s) recherchée(s).)
A l'aide du graphique, on peut en conclure que l'antécédent de par la fonction est .

Question 4
Déterminer graphiquement l'antécédent de par .
Correction
Ici, on souhaite déterminer l'antécédent de par la fonction , c'est-à-dire trouver la valeur de tel que . Pour cela :
On repère le point d'ordonnée , et ensuite, on rejoint la courbe horizontalement. (Cela revient à tracer la droite d'équation .)
Ensuite, au(x) point(s) d'intersection de la droite d'équation et de la courbe, on rejoint l'axe des abscisses. (En ce point se trouve la ou les valeur(s) recherchée(s).)
À l'aide du graphique, on peut en conclure que l'antécédent de par la fonction est .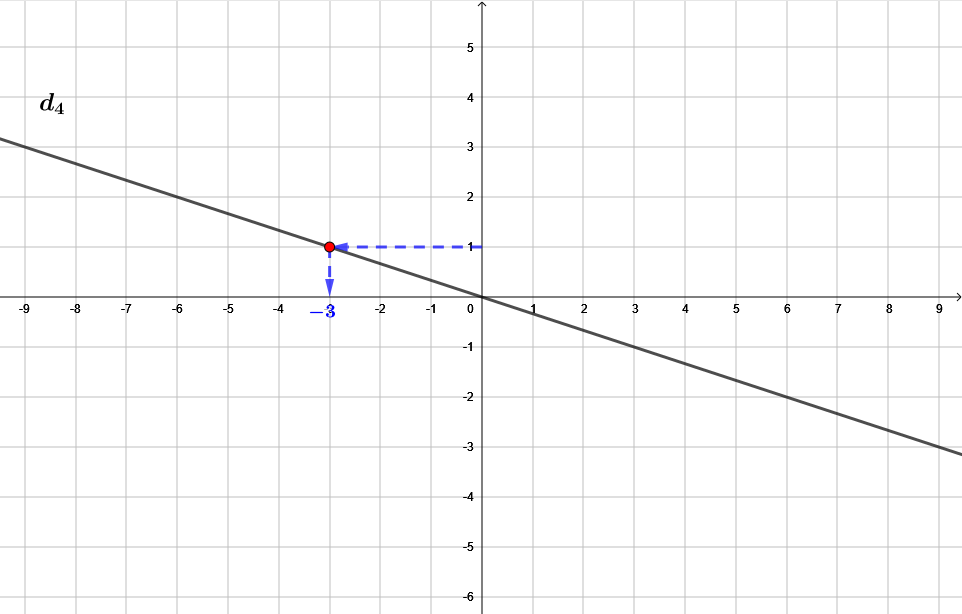
On repère le point d'ordonnée , et ensuite, on rejoint la courbe horizontalement. (Cela revient à tracer la droite d'équation .)
Ensuite, au(x) point(s) d'intersection de la droite d'équation et de la courbe, on rejoint l'axe des abscisses. (En ce point se trouve la ou les valeur(s) recherchée(s).)
À l'aide du graphique, on peut en conclure que l'antécédent de par la fonction est .

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.