Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ème partie - Exercice 1
15 min
25
Question 1
On représente droites ci-dessous :
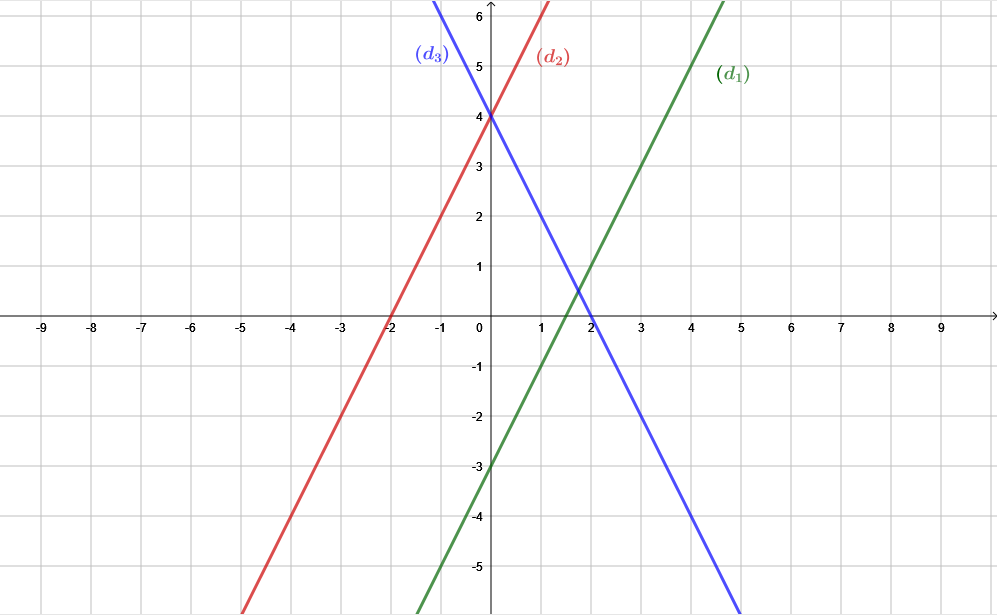

À l'aide du graphique ci-dessus, complétez le tableau suivant :
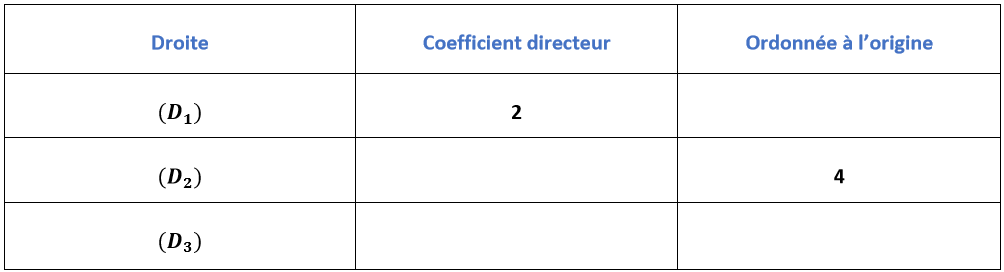

Correction
Déterminons dans un premier temps l'ordonnée à l'origine de et .
À l'aide du graphique ci-dessous, on constate que l'ordonnée à l'origine de la droite est .
On constate également que on la même ordonnée à l'origine qui est .
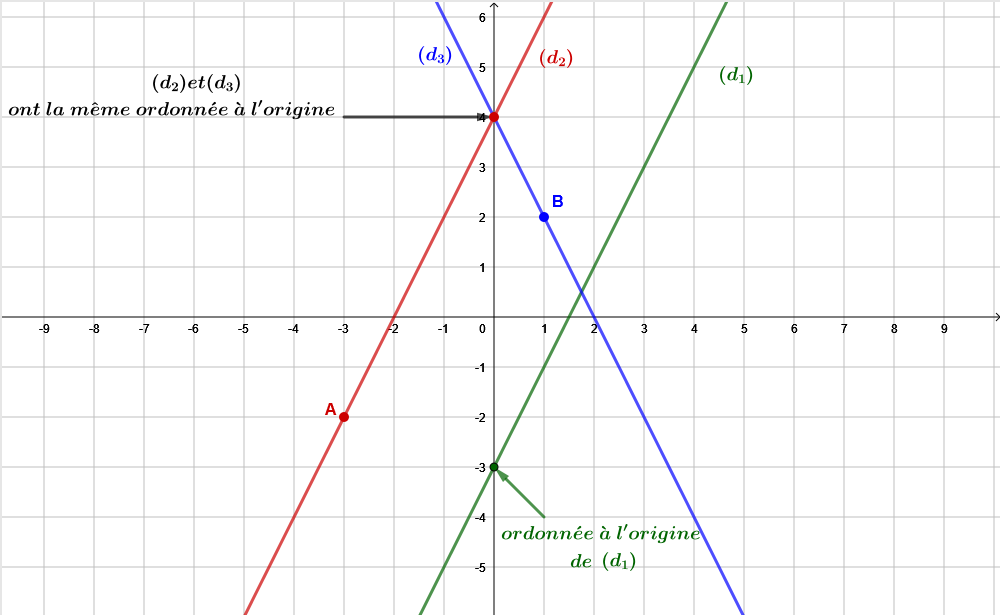
Déterminons dans un second temps les coefficients directeurs de etConcernant la droite , on considère points et représentés ci-dessous.
En partant du point :
On se déplace horizontalement de 1 unité, puis verticalement, on monte de 2 unités pour rejoindre le point .
Par conséquent :
Concernant la droite , on considère points et représentés ci-dessous.
En partant du point :
On se déplace horizontalement de 1 unité, puis verticalement, on monte de 2 unités pour rejoindre le point .
Par conséquent :
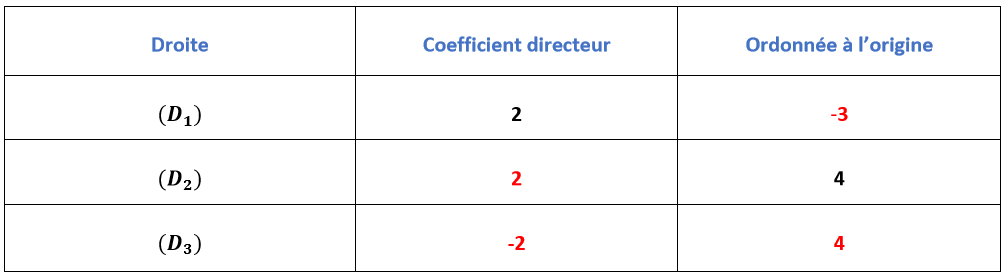
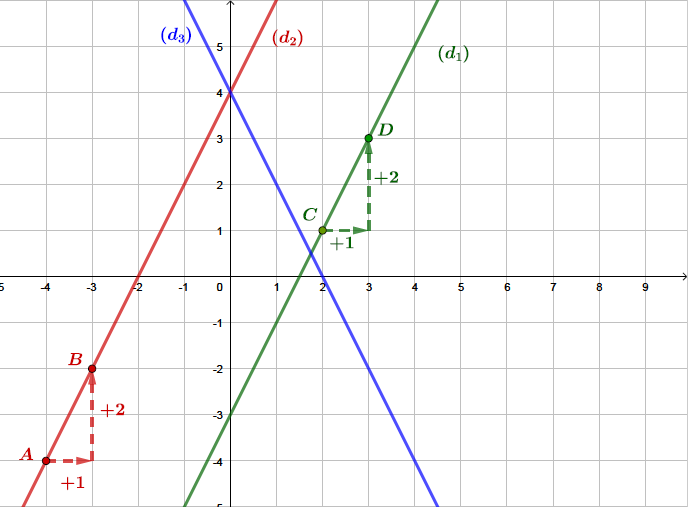 On peut donc remplir le tableau suivant :
On peut donc remplir le tableau suivant :
- Graphiquement, l'ordonnée à l'origine est la valeur de que l'on lit sur l'axe des ordonnées, lorsque
On constate également que on la même ordonnée à l'origine qui est .

Déterminons dans un second temps les coefficients directeurs de et
- Pour lire graphiquement le coefficient directeur d'une droite :
- On choisit deux points sur la droite. (De préférence des points aux coordonnées précises.
- Ensuite en partant d'un deux points :
On regarde de combien d'unités on doit se déplacer horizontalement et verticalement pour rejoindre le deuxième point. - Puis on détermine le coefficient directeur à l'aide de la formule :
En partant du point :
Par conséquent :
Concernant la droite , on considère points et représentés ci-dessous.
En partant du point :
Par conséquent :


Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.