Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Exercices types : 11ère partie - Exercice 3

10 min
20
Question 1
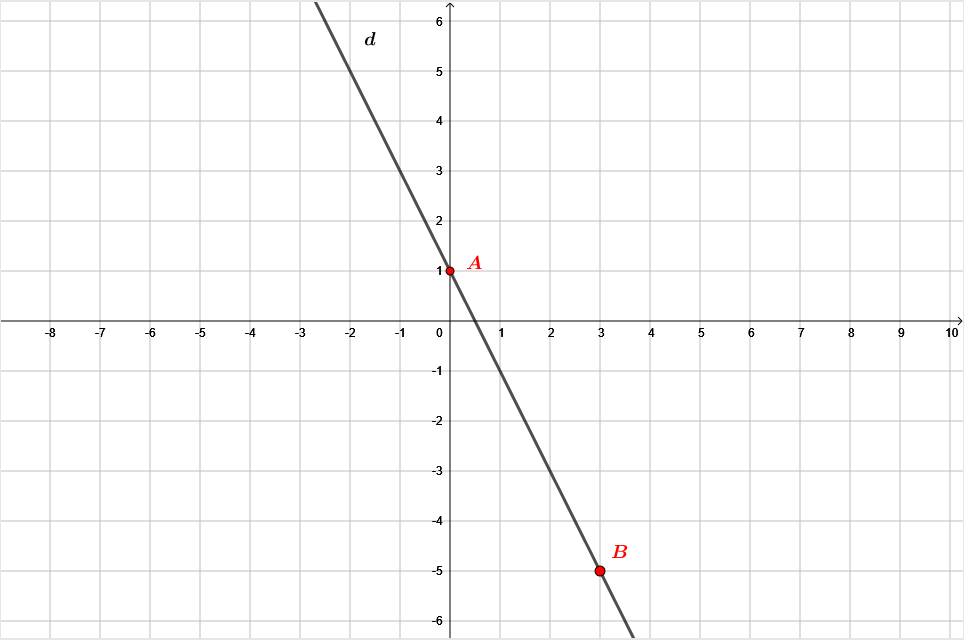
Une droite (d)(d) représente la fonction affine ff telle que f(x)=−2x+1f (x) = -2x+1.

Dans un repère, représenter graphiquement la droite (d)(d).

Correction
  • La représentation graphique d'une fonction affine est une droite.
  • Pour tracer une droite, il est nécessaire de connaitre au moins les coordonnées de 2 points de cette droite.
Pour tracer la droite (d)(d) on a besoin de 22 points :
  • Afin de déterminer les coordonnées d'un premier point de la droite (d)(d), il suffit de calculer l'image d'un point quelconque.
    Calculons ici l'image d'un premier point d’abscisse 0.
    Pour déterminer l'image de 00 par ff, il nous suffit de remplacer xx par 00.
    Il vient alors que :
    f(0)=−2×0+1f\left(0\right)=-2\times 0+1
    f(0)=1f\left(0\right)=1

    L'image de 00 par ff vaut 11 .
    Donc ici, on a bien les coordonnées d'un 1er1^{er} point : (0;1)\color{blue}(0;1).
    Calculons ici l'image d'un deuxième point d’abscisse 3.
    Pour déterminer l'image de 33 par ff, il nous suffit de remplacer xx par 33.
    (Ici, on peut choisir n'importe quel autre abscisse.)
    Il vient alors que :
    f(3)=−2×3+1f\left(3\right)=-2\times 3+1
    f(3)=−6+1f\left(3\right)=-6+1
    f(3)=−5f\left(3\right)=-5

    L'image de 33 par ff vaut −5-5.
    Donc ici, on a bien les coordonnées d'un 2eˋme2^{ème} points : (3;−5)\color{blue}(3;-5).
    • Question 2
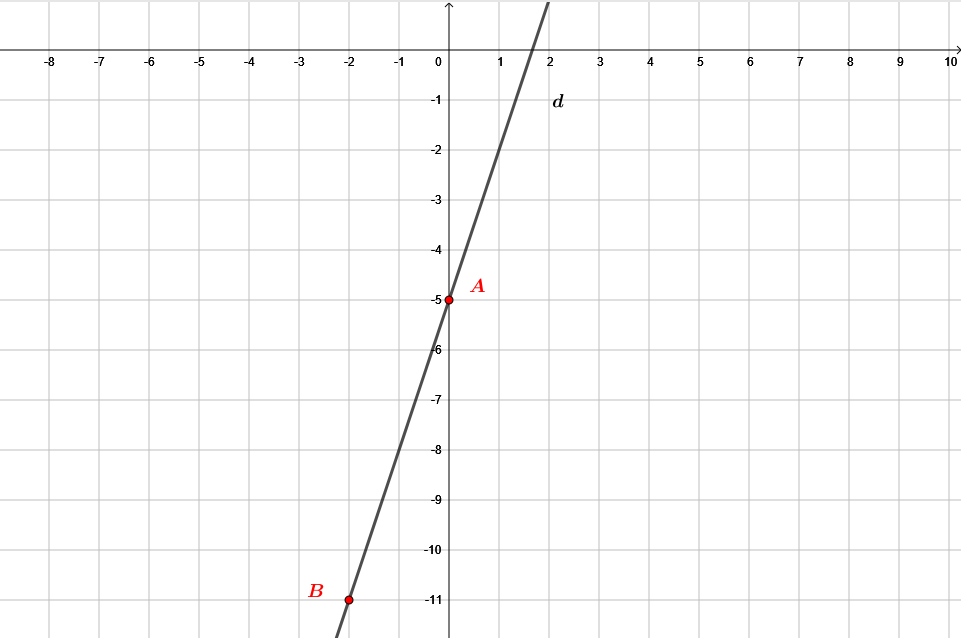
    Une droite (d)(d) représente la fonction affine ff telle que f(x)=3x−5f (x) = 3x-5

    Dans un repère, représenter graphiquement la droite (d)(d).

    Correction
    • La représentation graphique d'une fonction affine est une droite.
    • Pour tracer une droite, il est nécessaire de connaitre au moins les coordonnées de 2 points de cette droite.
    Pour tracer la droite (d)(d) on a besoin de 22 points :
  • Afin de déterminer les coordonnées d'un premier point de la droite (d)(d), il suffit de calculer l'image d'un point quelconque.
    Calculons ici l'image d'un premier point d’abscisse 0.
    Pour déterminer l'image de 00 par ff, il nous suffit de remplacer xx par 00.
    Il vient alors que :
    f(0)=3×0−5f\left(0\right)=3\times 0-5
    f(0)=−5f\left(0\right)=-5

    L'image de 00 par ff vaut −5-5 .
    Donc ici, on a bien les coordonnées d'un 1er1^{er} point : (0;−5)\color{blue}(0;-5).
    Calculons ici l'image d'un deuxième point d’abscisse −‾\underline{-}2 :
    (Ici, on peut choisir n'importe quel autre abscisse.)
    Pour déterminer l'image de −2-2 par ff, il nous suffit de remplacer xx par −2-2.
    Il vient alors que :
    f(−2)=3×(−2)−5f\left(-2\right)=3\times (-2)-5
    f(−2)=−6−5f\left(-2\right)=-6-5
    f(−2)=−11f\left(-2\right)=-11

    L'image de −2-2 par ff vaut −11-11.
    Donc ici, on a bien les coordonnées d'un 2eˋme2^{ème} points : (−2;−11)\color{blue}(-2;-11).

    • Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.