Savoir résoudre des problèmes se ramenant à des équations du premier degré - Exercice 4
14 min
25
COMPETENCES:
1°) Résoudre des problèmes, analyser et exploiter ses erreurs.
2°) Savoir résoudre une équation et calculer en utilisant le langage algébrique. (Lettres, symboles, etc).
1°) Résoudre des problèmes, analyser et exploiter ses erreurs.
2°) Savoir résoudre une équation et calculer en utilisant le langage algébrique. (Lettres, symboles, etc).
Question 1
On propose deux programmes de calculs ci-dessous :
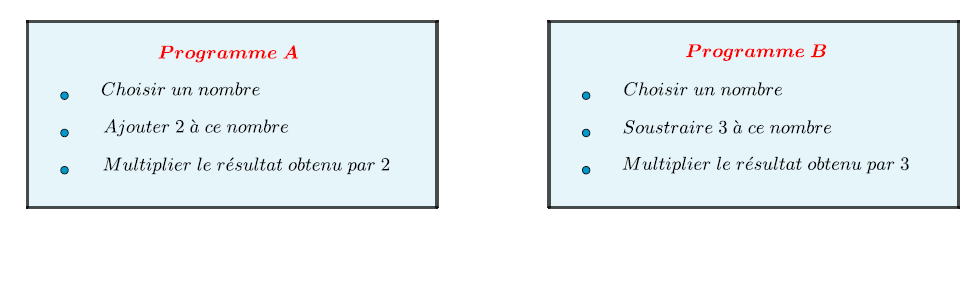
Exprimer en fonction de le nombre obtenu à l'issue du programme de calcul .
Correction
1°) Déterminons le résultat obtenu en fonction de x pour le programme A :
première étape :
Le nombre choisi est
deuxième étape :
On ajoute à ce nombre. C'est-à-dire additionner à .
On obtient donc
troisième étape :
On doit ici multiplier le résultat obtenu par , c'est-à-dire :
Ici, il faut bien faire attention de mettre (x+2) entre parenthèses.
En effet :
On obtient donc
On peut donc conclure que
première étape :
Le nombre choisi est
deuxième étape :
On ajoute à ce nombre. C'est-à-dire additionner à .
On obtient donc
troisième étape :
On doit ici multiplier le résultat obtenu par , c'est-à-dire :
Ici, il faut bien faire attention de mettre (x+2) entre parenthèses.
En effet :
On obtient donc
On peut donc conclure que
Question 2
Exprimer en fonction de le nombre obtenu à l'issue du programme de calcul .
Correction
2)° Déterminons le résultat obtenu en fonction de x pour le programme B :
première étape :
Le nombre choisi est
deucième étape :
On soustrait à ce nombre. C'est-à-dire soustraire à .
On obtient donc
troisième étape :
On doit ici multiplier le résultat obtenu par , c'est-à-dire :
Ici, il faut bien faire attention de mettre (x-3) entre parenthèses.
En effet :
On obtient donc
On peut donc conclure que
première étape :
Le nombre choisi est
deucième étape :
On soustrait à ce nombre. C'est-à-dire soustraire à .
On obtient donc
troisième étape :
On doit ici multiplier le résultat obtenu par , c'est-à-dire :
Ici, il faut bien faire attention de mettre (x-3) entre parenthèses.
En effet :
On obtient donc
On peut donc conclure que
Question 3
Pour quel nombre choisi au départ le résultat obtenu au programme est égal au résultat obtenu au programme .
Correction
Avoir le même résultat à l'issue des deux programmes signifie que :
Or et . Par conséquent, on doit résoudre l'équation suivante :
. On soustrait à chaque membre.
. On soustrait à chaque membre.
. On divise chaque membre par le nombre devant le qui ici vaut .
Ainsi :
On peut donc conclure que le nombre à choisir pour obtenir le même résultat à l'issue des 2 programmes est
Or et . Par conséquent, on doit résoudre l'équation suivante :
- On doit dans un premier temps rassembler les termes en dans le membre de gauche.
. On soustrait à chaque membre.
. On soustrait à chaque membre.
. On divise chaque membre par le nombre devant le qui ici vaut .
Ainsi :
On peut donc conclure que le nombre à choisir pour obtenir le même résultat à l'issue des 2 programmes est
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.