Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Mesure d'un angle orienté - Exercice 1
10 min
25
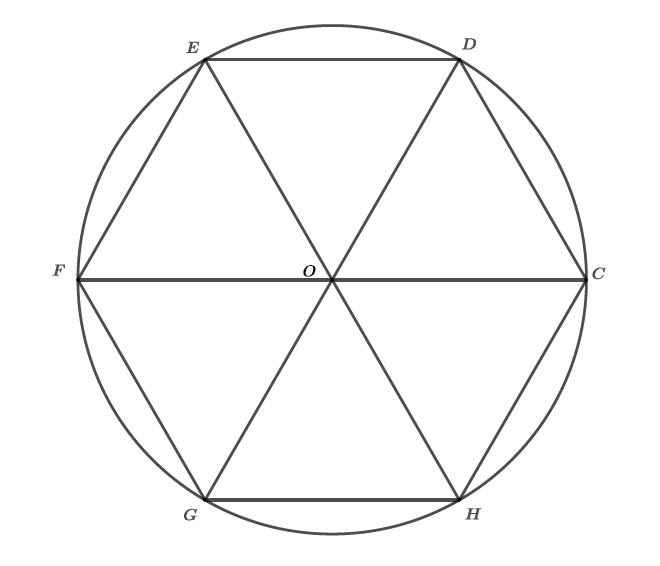
A l'intérieur du cercle trigonométrique, nous dessinons un hexagone régulier noté .
Question 1
Correction
Les angles ; ; ; ; et sont appelés des angles au centre.
L'hexagone régulier a donc cotés . Pour déterminer la mesure d'un angle au centre de cet hexagone, il suffit d'appliquer la formule du rappel c'est à dire
Nous voulons déterminer la mesure de l'angle orienté . Il s'agit de la mesure de l'angle et nous sommes dans le car nous allons de vers .
Il en résulte donc que : 
Nous voulons déterminer la mesure de l'angle orienté . Il s'agit de la mesure de l'angle et nous sommes dans le car nous allons de vers .
Il en résulte donc que :

Question 2
Correction
Les angles ; ; ; ; et sont appelés des angles au centre.
L'hexagone régulier a donc cotés . Pour déterminer la mesure d'un angle au centre de cet hexagone, il suffit d'appliquer la formule du rappel c'est à dire
Nous voulons déterminer la mesure de l'angle orienté . Il s'agit de la mesure de l'angle et nous sommes dans le car nous allons de vers .
Il en résulte donc que :
Nous voulons déterminer la mesure de l'angle orienté . Il s'agit de la mesure de l'angle et nous sommes dans le car nous allons de vers .
Il en résulte donc que :

Question 3
Correction
Les angles ; ; ; ; et sont appelés des angles au centre.
L'hexagone régulier a donc cotés . Pour déterminer la mesure d'un angle au centre de cet hexagone, il suffit d'appliquer la formule du rappel c'est à dire
Nous voulons déterminer la mesure de l'angle orienté . Il s'agit de la mesure de l'angle et nous sommes dans le car nous allons de vers .
De plus :
. Or nous avons vu précédemment que les angles au centre de cet hexagone mesuraient tous radians
Il en résulte donc que :
Nous voulons déterminer la mesure de l'angle orienté . Il s'agit de la mesure de l'angle et nous sommes dans le car nous allons de vers .
De plus :
. Or nous avons vu précédemment que les angles au centre de cet hexagone mesuraient tous radians
Il en résulte donc que :

Question 4
Correction
Les angles ; ; ; ; et sont appelés des angles au centre.
L'hexagone régulier a donc cotés . Pour déterminer la mesure d'un angle au centre de cet hexagone, il suffit d'appliquer la formule du rappel c'est à dire
Nous voulons déterminer la mesure de l'angle orienté . Il s'agit de la mesure de l'angle et nous sommes dans le car nous allons de vers .
De plus :
. Or nous avons vu précédemment que les angles au centre de cet hexagone mesuraient tous radians
Il en résulte donc que :
Nous voulons déterminer la mesure de l'angle orienté . Il s'agit de la mesure de l'angle et nous sommes dans le car nous allons de vers .
De plus :
. Or nous avons vu précédemment que les angles au centre de cet hexagone mesuraient tous radians
Il en résulte donc que :

Question 5
Correction
Les angles ; ; ; ; et sont appelés des angles au centre.
L'hexagone régulier a donc cotés . Pour déterminer la mesure d'un angle au centre de cet hexagone, il suffit d'appliquer la formule du rappel c'est à dire
Nous voulons déterminer la mesure de l'angle orienté . Il s'agit de la mesure de l'angle et nous sommes dans le car nous allons de vers .
De plus :
. Or nous avons vu précédemment que les angles au centre de cet hexagone mesuraient tous radians
Il en résulte donc que :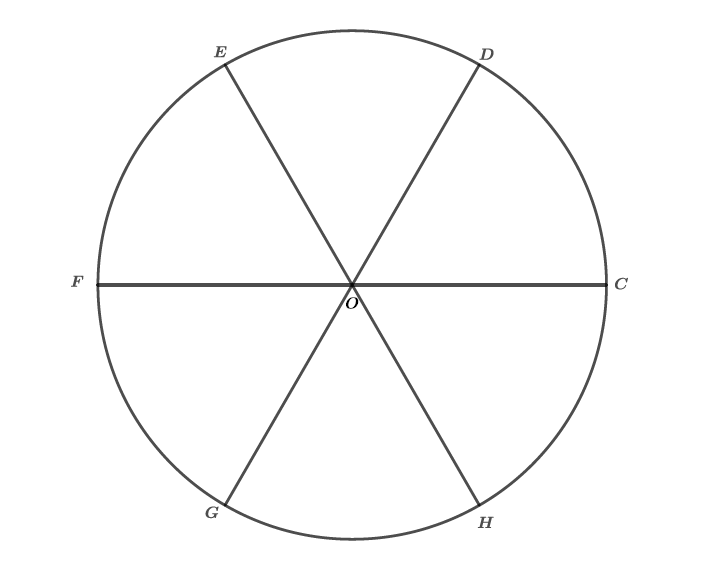
Nous voulons déterminer la mesure de l'angle orienté . Il s'agit de la mesure de l'angle et nous sommes dans le car nous allons de vers .
De plus :
. Or nous avons vu précédemment que les angles au centre de cet hexagone mesuraient tous radians
Il en résulte donc que :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.