Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : 2ème partie - Exercice 1
21 min
40
Une entreprise produit et vend du safran, une épice de grande qualité. On note le nombre de kilogrammes que produit et vend l’entreprise en un an, étant compris entre et . Le montant des charges correspondant à la production de kilogrammes de safran, exprimé en milliers d’euros, est modélisé par la fonction définie sur l’intervalle par : .
On a tracé ci-dessous la représentation graphique de cette fonction dans un repère orthogonal.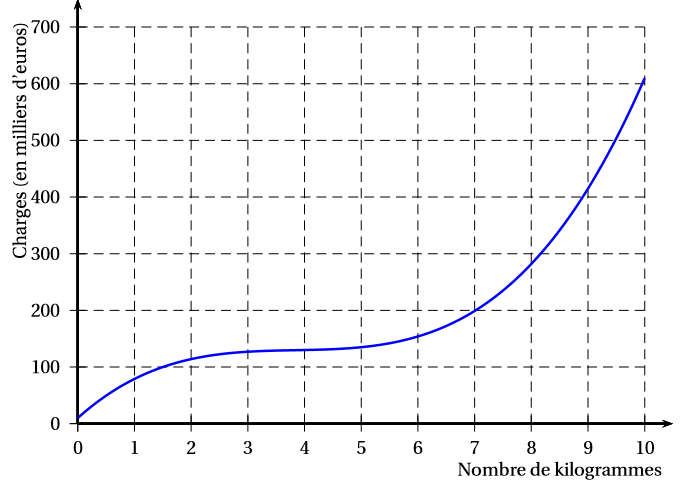
On a tracé ci-dessous la représentation graphique de cette fonction dans un repère orthogonal.

Question 1
Déterminer le montant des charges lorsque l’entreprise produit kilogrammes de safran.
Correction
Le montant des charges lorsque l’entreprise produit kilogrammes de safran est milliers d’euros.
Comme alors :
Finalement, le montant des charges est de euros.
Comme alors :
Finalement, le montant des charges est de euros.
Question 2
Déterminer, par lecture graphique, le nombre de kilogrammes de safran à produire pour que le montant des charges soit égal à
euros.
euros.
Correction
Le nombre de kilogrammes de safran à produire pour que le montant des charges soit égal à euros est environ . (voir graphique).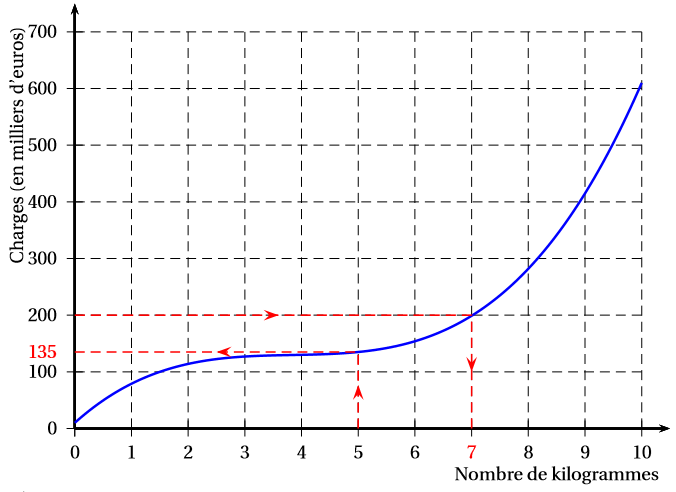

Question 3
L’entreprise vend la totalité de sa production. Chaque kilogramme de safran est vendu au prix de milliers d’euros.
Déterminer le chiffre d’affaires , en milliers d’euros, réalisé pour la vente de kilogrammes de safran.
Correction
Chaque kilogramme de safran est vendu au prix de milliers d’euros.
Ainsi, le chiffre d’affaires , en milliers d’euros, réalisé pour la vente de kilogrammes de safran est .
Ainsi, le chiffre d’affaires , en milliers d’euros, réalisé pour la vente de kilogrammes de safran est .
Question 4
Vérifier que le bénéfice , en milliers d’euros, réalisé pour la vente de kilogrammes de safran est : .
Correction
- Bénéfice Recette Coût de production
équivaut successivement à :
Question 5
On note la fonction dérivée de la fonction .
Calculer .
Correction
Question 6
Montrer que peut s'écrire sous la forme :
Correction
Nous voulons obtenir :
Pour cela nous allons développer l'expression donnée .
Il vient alors que :
Ainsi :
Pour cela nous allons développer l'expression donnée .
Il vient alors que :
Ainsi :
Question 7
Étudier le signe de . Donner le tableau de variation de .
Correction
D'après la question précédente, nous savons que :
Ainsi :
Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
Enfin, est strictement négatif. On mettra que le signe dans la ligne de .
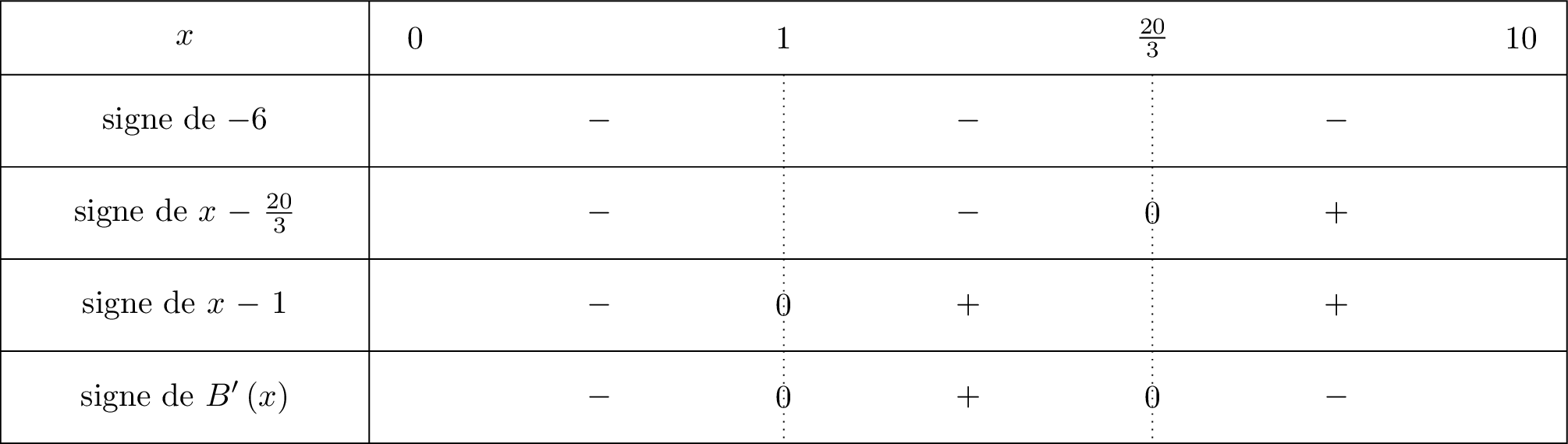
Ainsi :
Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
Enfin, est strictement négatif. On mettra que le signe dans la ligne de .

Question 8
Dresser le tableau de variation de sur l'intervalle .
Correction
- Si est négative sur alors est décroissante sur .
- Si est positive sur alors est croissante sur .
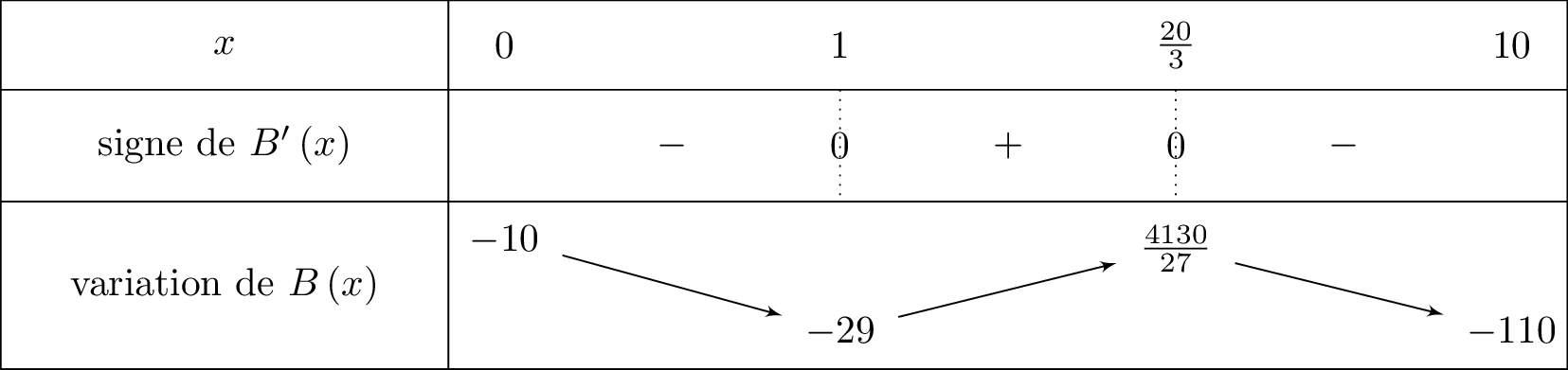
Question 9
Quelle quantité de safran l’entreprise doit-elle vendre pour réaliser le bénéfice maximal? Quel est ce bénéfice maximal, arrondi au millier d’euros
Correction
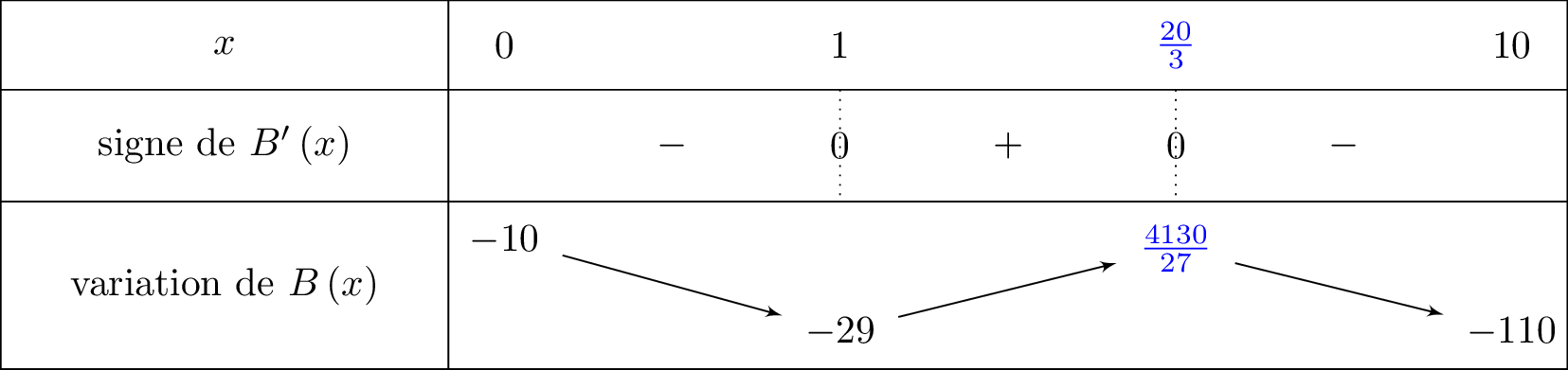
kg. Le bénéfice maximal est, arrondi au millier d’euro, de milliers d’euros. En effet :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.