Variables aléatoires

Répétition d’épreuves aléatoires de Bernoulli - Exercice 1

10 min
25
Question 1
Une urne dispose de 1010 boules dont 88 blanches et 22 noires. Après chaque tirage, on remet la boule tirée dans l'urne. On effectue trois tirages. On tire une boule blanche 88 fois sur 1010. On note BB la probabilité de tirer une boule blanche

Expliquer pourquoi on peut modéliser les trois tirages par une répétition d’épreuves de Bernoulli.

Correction
  • Une épreuve de Bernoulli de paramètre pp est une expérience aléatoire n’ayant que deux issues\text{\red{issues}}.
    • L’expérience aléatoire a deux issues\text{\red{issues}} : « Tirer une boule blanche » et « Tirer une boule noire ». C’est donc une épreuve de Bernoulli.
    Son paramètre est la probabilité que la boule tirée soit blanche c'est à dire p=410=25p=\frac{4}{10}=\frac{2}{5}
    Cela signifie qu'un tirage d'une boule dans l'urne est une épreuve de Bernoulli.
    On effectue trois tirages. On répète, donc, de façon identique et indeˊpendante\text{\red{identique et indépendante}} 33 épreuves de Bernoulli.
    Question 2

    Etablir l'arbre correspondant à la situation.

    Correction
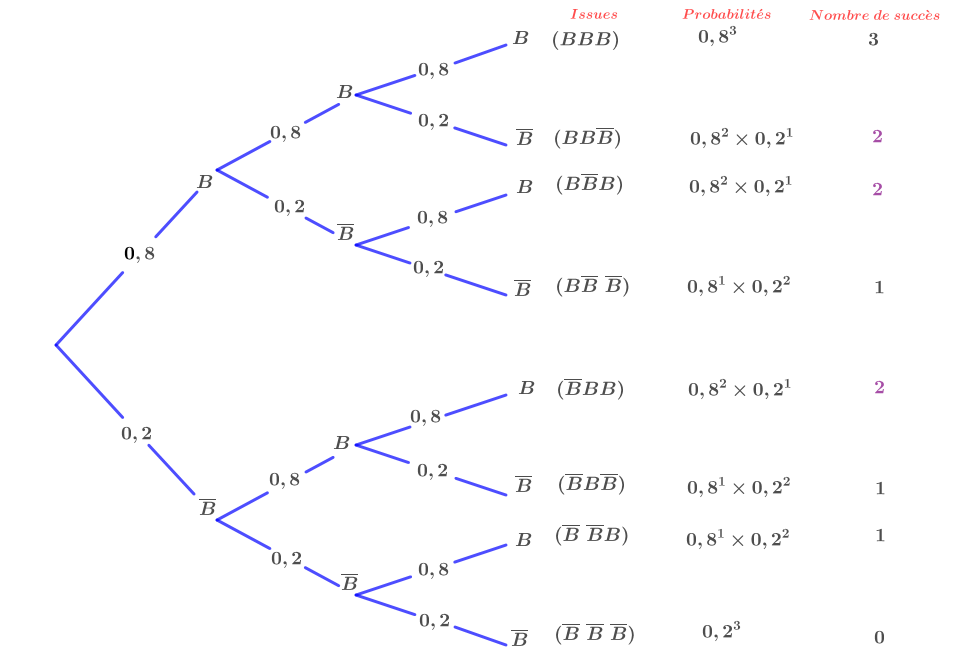
    Question 3

    Calculer la probabilité de tirer deux boules blanches. On notera maintenant XX la variable aléatoire associant le nombre de boules blanches tirées lors des 33 tirages.

    Correction
    La probabilité d’un événement correspondant à un chemin sur un arbre est donnée par le produit des probabilités rencontrées le long du chemin . Nous voulons avoir 22 boules blanches.
    Il nous faut donc choisir les chemins qui ont un nombres de succès égale à 22 que nous avons mis en violet\text{\purple{violet}} .
    On notera alors :
    P(X=2)=P(BBB‾)+P(BB‾B)+P(B‾BB)P\left(X=2\right)=P\left(BB\overline{B}\right)+P\left(B\overline{B}B\right)+P\left(\overline{B}BB\right)
    P(X=2)=0,82×0,21+0,82×0,21+0,82×0,21P\left(X=2\right)=0,8^2\times0,2^1+0,8^2\times0,2^1+0,8^2\times0,2^1
    P(X=2)=0,384P\left(X=2\right)=0,384