Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Variations des fonctions polynômes du troisième degré - Exercice 2
8 min
15
Question 1
Soit la fonction définie par sur l'intervalle .
Déterminer la dérivée de sur l'intervalle , et montrer que .
Correction
Nous voulons obtenir : .
Pour cela nous allons développer l'expression donnée .
Il vient alors que :
Ainsi :
Question 2
Dresser le tableau de signe de sur l'intervalle .
Correction
Nous savons que : . Nous allons donc dresser le tableau de signe de qui nous donnera ensuite les variations de .
Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
Et enfin, le coefficient est strictement positif, c'est à dire que dans la ligne de on ne mettra que le signe .
Il vient alors que :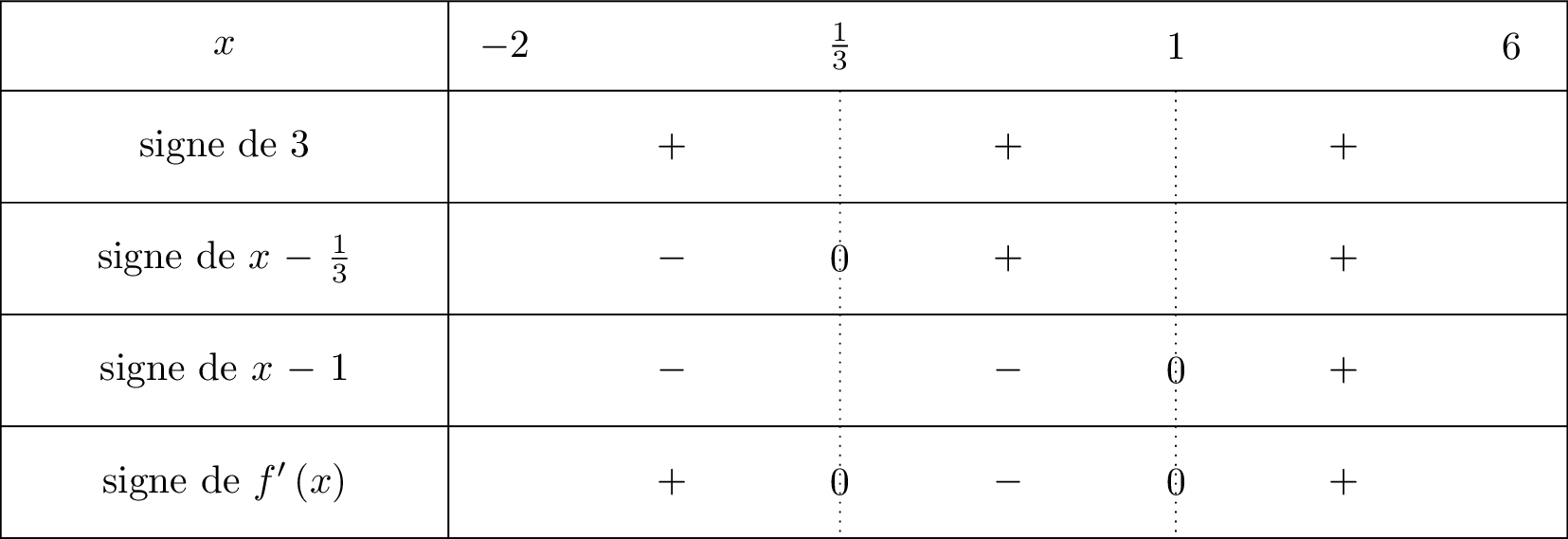
Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
Et enfin, le coefficient est strictement positif, c'est à dire que dans la ligne de on ne mettra que le signe .
Il vient alors que :

Question 3
Étudier les variations de la fonction sur l’intervalle .
Correction
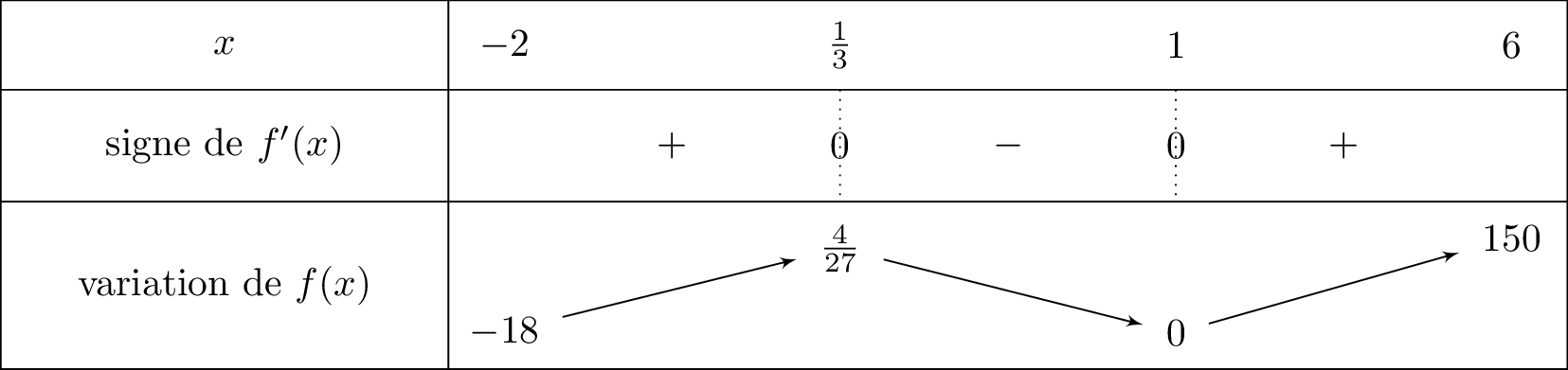
- Si est négative sur alors est décroissante sur .
- Si est positive sur alors est croissante sur .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.