Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Petits problèmes.... - Exercice 5
15 min
30
Adam dispose, dans sa collection, de cartes de basket NBA dont sont écrites en Anglais, les autres en Français ou en Espagnol. Il y a cinq fois plus de cartes françaises qu'anglaises.
Il décide de proposer un jeu à la fête de son école. La personne doit tirer une carte au hasard :
– si la carte tirée est en espagnol, le joueur perd pièces de euro,
– si la carte tirée est en Français, le joueur perd pièces de euro,
– si la carte tirée est en Anglais, Adam donne , au joueur, pièces de euro,
Bien entendu, .
On note la variable aléatoire correspondant au gain obtenu par Adam à ce jeu.
Il décide de proposer un jeu à la fête de son école. La personne doit tirer une carte au hasard :
– si la carte tirée est en espagnol, le joueur perd pièces de euro,
– si la carte tirée est en Français, le joueur perd pièces de euro,
– si la carte tirée est en Anglais, Adam donne , au joueur, pièces de euro,
Bien entendu, .
On note la variable aléatoire correspondant au gain obtenu par Adam à ce jeu.
Question 1
Pour les questions et , on suppose que .
Déterminer la loi de probabilité de .
Déterminer la loi de probabilité de .
Correction
Nous savons qu'il y a de cartes anglais.
Il y a cinq fois plus de cartes françaises qu'anglaises. Cela signifie que l'on a de cartes françaises.
Finalement, il y a de cartes espagnoles.
La loi de probabilité de est donnée ci-dessous :
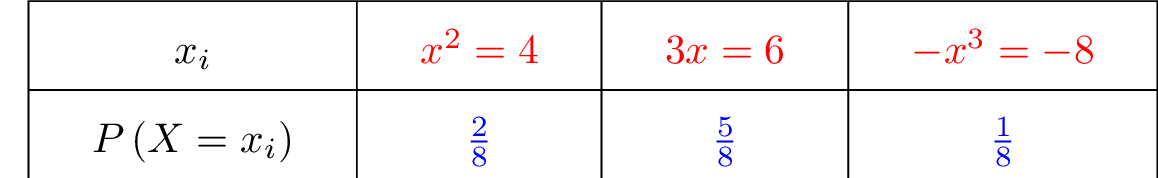
Il y a cinq fois plus de cartes françaises qu'anglaises. Cela signifie que l'on a de cartes françaises.
Finalement, il y a de cartes espagnoles.
La loi de probabilité de est donnée ci-dessous :
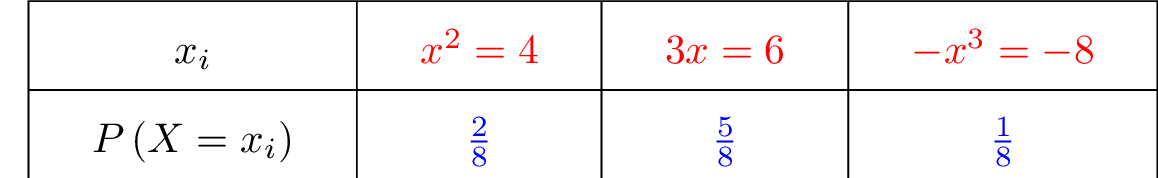
Question 2
Pour les questions et , on suppose que .
Quel est le gain moyen de ce jeu ? Quelle interprétation peut-on en faire ?
Quel est le gain moyen de ce jeu ? Quelle interprétation peut-on en faire ?
Correction
On appelle l’espérance mathématique de la variable , la quantité notée définie par :
Ainsi :
En moyenne, Adam gagnera euros.
Question 3
On cherche à déterminer la valeur de telle que le gain moyen réalisé sur un grand nombre de tirages soit maximal.
Montrer que le problème posé revient à étudier les variations de la fonction définie sur par :
Correction
Nous allons donner la loi de probabilité de , en ne donnant pas de valeurs particulières à . Il vient alors que :
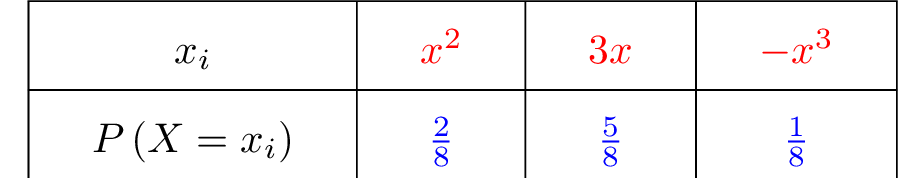 Nous allons calculer l'espérance de , que l'on notera . Il s'ensuit que :
Nous allons calculer l'espérance de , que l'on notera . Il s'ensuit que :
Enfin :
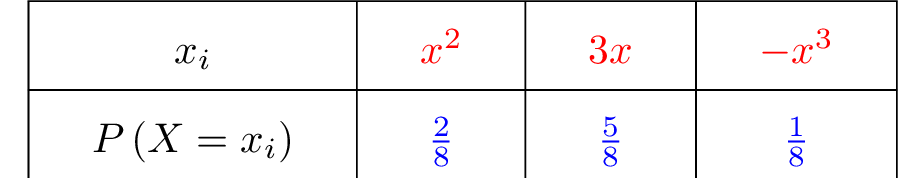
Enfin :
Question 4
Étudier les variations de sur .
Correction
Trouver la valeur de pour laquelle le gain moyen est maximal revient donc à étudier l'existence d'un maximum pour la fonction .
est dérivable sur .
On a alors :
est une fonction trinôme du second degré. Nous allons déterminer son discriminant.
Alors ; et .
Or donc .
Il existe donc deux racines réelles distinctes.
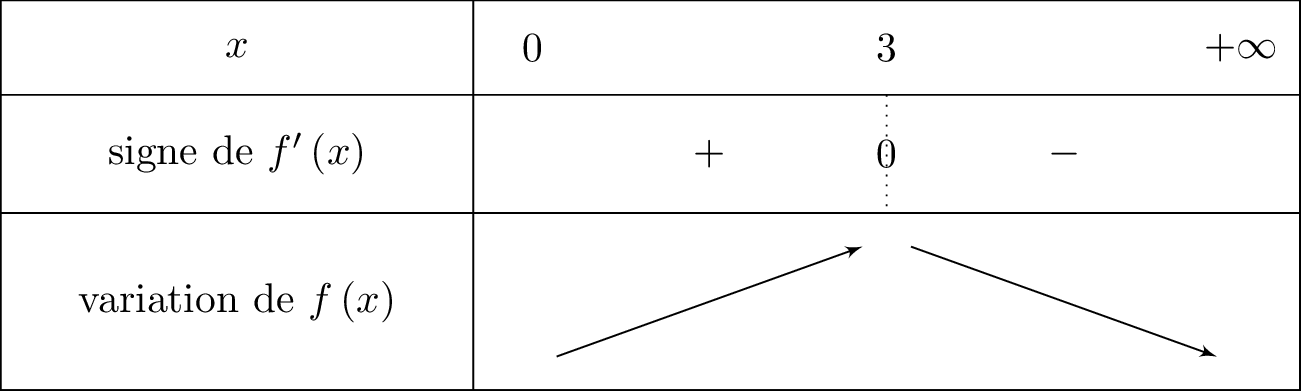
On en déduit le tableau de variation suivant :
est dérivable sur .
On a alors :
est une fonction trinôme du second degré. Nous allons déterminer son discriminant.
Alors ; et .
Or donc .
Il existe donc deux racines réelles distinctes.
- ce qui donne .
- ce qui donne .
On en déduit le tableau de variation suivant :

Question 5
Déterminer . En déduire le gain moyen maximal de ce jeu.
Correction
admet donc un maximum en .
Pour obtenir la valeur du maximum, il nous suffit de calculer
Ainsi :
Le gain moyen maximal du jeu est donc de euros.
Pour obtenir la valeur du maximum, il nous suffit de calculer
Ainsi :
Le gain moyen maximal du jeu est donc de euros.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.