Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Exercices types : 33ème partie - Exercice 1

20 min
40
Un magasin de téléphonie mobile lance une offre sur ses smartphones de la marque Pomme vendus à 800800 € : il propose une assurance complémentaire pour 5050 € ainsi qu’une coque à 2020 €.
Ce magasin a fait les constatations suivantes concernant les acheteurs de ce smartphone :
  • 40%40\% des acheteurs ont souscrit à l’assurance complémentaire.
  • Parmi les acheteurs qui ont souscrit à l’assurance complémentaire, 20%20\% ont acheté en plus la coque.
  • Parmi les acheteurs qui n’ont pas souscrit à l’assurance complémentaire, deux sur trois n’ont pas acheté la coque.
    • On interroge au hasard un client de ce magasin ayant acheté un smartphone de la marque Pomme.
    On considère les évènements suivants :
    AA : « le client a souscrit à l’assurance complémentaire » ;
    CC : « le client a acheté la coque ».
    Question 1

    Construire un arbre pondéré traduisant la situation.

    Correction
    On peut dresser l’arbre pondéré de probabilités :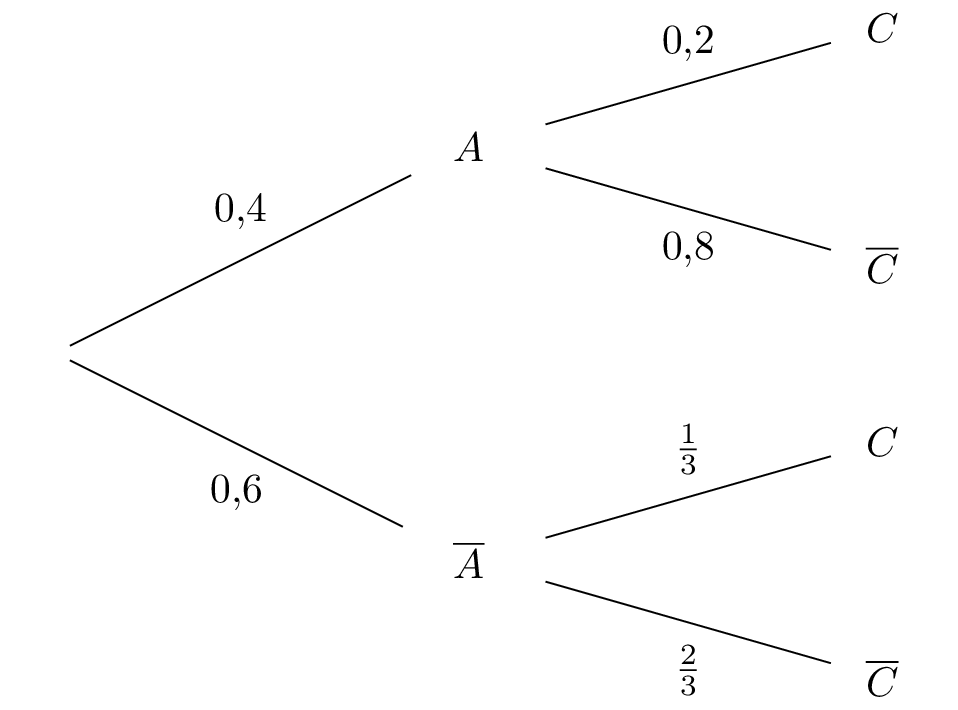
    Question 2

    Calculer la probabilité que le client ait souscrit à l’assurance complémentaire et ait acheté la coque.

    Correction
    P(A∩C)=P(A)×PA(C)P\left(A\cap C\right)=P\left(A\right)\times P_{A} \left(C\right)
    P(A∩C)=0,4×0,2P\left(A\cap C\right)=0,4\times 0,2
    Ainsi :
    P(A∩C)=0,08P\left(A\cap C\right)=0,08

    Question 3

    Montrer que P(C)=0,28P\left(C\right) = 0,28.

    Correction
    AA et A‾\overline{A} forment une partition de l'univers.
    D'après la formule des probabilités totales on a :
    P(C)=P(A∩C)+P(A‾∩C)P\left(C\right)=P\left(A\cap C\right)+P\left(\overline{A}\cap C\right)
    P(C)=P(A)×PA(C)+P(A‾)×PA‾(C)P\left(C\right)=P\left(A\right)\times P_{A} \left(C\right)+P\left(\overline{A}\right)\times P_{\overline{A}} \left(C\right)
    P(C)=0,4×0,2+0,6×13P\left(C\right)=0,4\times 0,2+0,6\times \frac{1}{3}
    P(C)=0,08+0,2P\left(C\right)=0,08+0,2
    Ainsi :
    P(C)=0,28P\left(C\right)=0,28

    Question 4

    Le client interrogé a acheté la coque.
    Quelle est la probabilité qu’il n’ait pas souscrit à l’assurance complémentaire ?

    Correction
    On pourrait traduire la question de la manière suivante ; sachant{\color{blue}{\text{sachant}}} que client interrogé a acheté la coque, quelle est la probabilité qu’il n’ait pas souscrit à l’assurance complémentaire ?
      On note PB(A)P_{B} \left(A\right) la probabilité d’avoir l’événement AA sachant que l’événement BB est réalisé. On a alors la relation suivante :
    • PB(A)=P(A∩B)P(B)P_{B} \left(A\right)=\frac{P\left(A\cap B\right)}{P\left(B\right)}
    Il vient alors que :
    PC(A‾)=P(A‾∩C)P(C)P_{C} \left(\overline{A}\right)=\frac{P\left(\overline{A}\cap C\right)}{P\left(C\right)}
    PC(A‾)=P(A‾)×PA‾(C)P(C)P_{C} \left(\overline{A}\right)=\frac{P\left(\overline{A}\right)\times P_{\overline{A}} \left(C\right)}{P\left(C\right)}
    PC(A‾)=0,6×130,28P_{C} \left(\overline{A}\right)=\frac{0,6\times \frac{1}{3} }{0,28}
    PC(A‾)=0,20,28P_{C} \left(\overline{A}\right)=\frac{0,2}{0,28}
    D'où :
    PC(A‾)=57P_{C} \left(\overline{A}\right)=\frac{5}{7}
    Question 5

    Déterminer la dépense moyenne d’un client de ce magasin ayantacheté un smartphone de la marque Pomme.
    On pourra noter XX la variable aléatoire qui représente la dépense en euros d’un client de ce magasin ayant acheté un smartphone de la marque Pomme.

    Correction
  • L'évènement A∩CA\cap C correspond à un client qui a souscrit une assurance complémentaire et qui a acheté la coque . La dépense est alors de 800+50+20=870800+50+20=870 euros. De plus : P(A∩C)=0,4×0,2=0,08P\left(A\cap C\right)=0,4\times0,2=0,08
  • L'évènement A∩C‾A\cap \overline{C} correspond à un client qui a souscrit une assurance complémentaire et qui n'a pas acheté la coque . La dépense est alors de 800+50=850800+50=850 euros. De plus : P(A∩C‾)=0,4×0,8=0,32P\left(A\cap \overline{C}\right)=0,4\times0,8=0,32
  • L'évènement A‾∩C\overline{A}\cap C correspond à un client qui n'a pas souscrit une assurance complémentaire et qui a acheté la coque . La dépense est alors de 800+20=820800+20=820 euros. De plus : P(A‾∩C)=0,6×13=0,2P\left(\overline{A}\cap C\right)=0,6\times \frac{1}{3}=0,2
  • L'évènement A‾∩C‾\overline{A}\cap \overline{C} correspond à un client qui a souscrit une assurance complémentaire et qui a acheté la coque . La dépense est alors de 800800 euros. De plus : P(A‾∩C‾)=0,6×23=0,4P\left(\overline{A}\cap \overline{C}\right)=0,6\times \frac{2}{3}=0,4
    • XX peut prendre les valeurs : 870870, 850850, 820820 et 800800 avec les probabilités respectives 0,080,08; 0,320,32; 0,20,2; 0,40,4.
    La dépense moyenne par client ayant acheté un smartphone de la marque Pomme est donc :
    La dépense moyenne par client ayant acheté un smartphone de la marque Pomme correspond à l'espérance de la variable aléatoire XX.
    On appelle l’espérance mathématique de la variable XX, la quantité notée E(X)E\left(X\right) définie par :
    • E(X)=∑xi×pi=x1×p1+x2×p2+…+xn×pnE\left(X\right)=\sum x_{i} \times p_{i} =x_{1} \times p_{1}+x_{2} \times p_{2}+\ldots+ x_{n} \times p_{n}
    E(X)=∑xi×piE\left(X\right)=\sum x_{i} \times p_{i}
    E(X)=800×0,4+820×0,2+850×0,32+870×0,08E\left(X\right)=800\times 0,4+820\times 0,2+850\times 0,32+870\times 0,08
    E(X)=825,6E\left(X\right)=825,6

    La dépense moyenne par client ayant acheté un smartphone de la marque Pomme est donc de 825,6825,6 €

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.