Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ème partie - Exercice 2
25 min
45
Question 1
Soit un entier naturel. Une urne contient une boule noire, deux boules vertes et boules rouges. On tire successivement et avec remise deux boules de l’urne.
Dresser un arbre pondéré traduisant la situation.
Correction
Il y a une boule noire, deux boules vertes et boules rouges, donc au total nous avons boules.
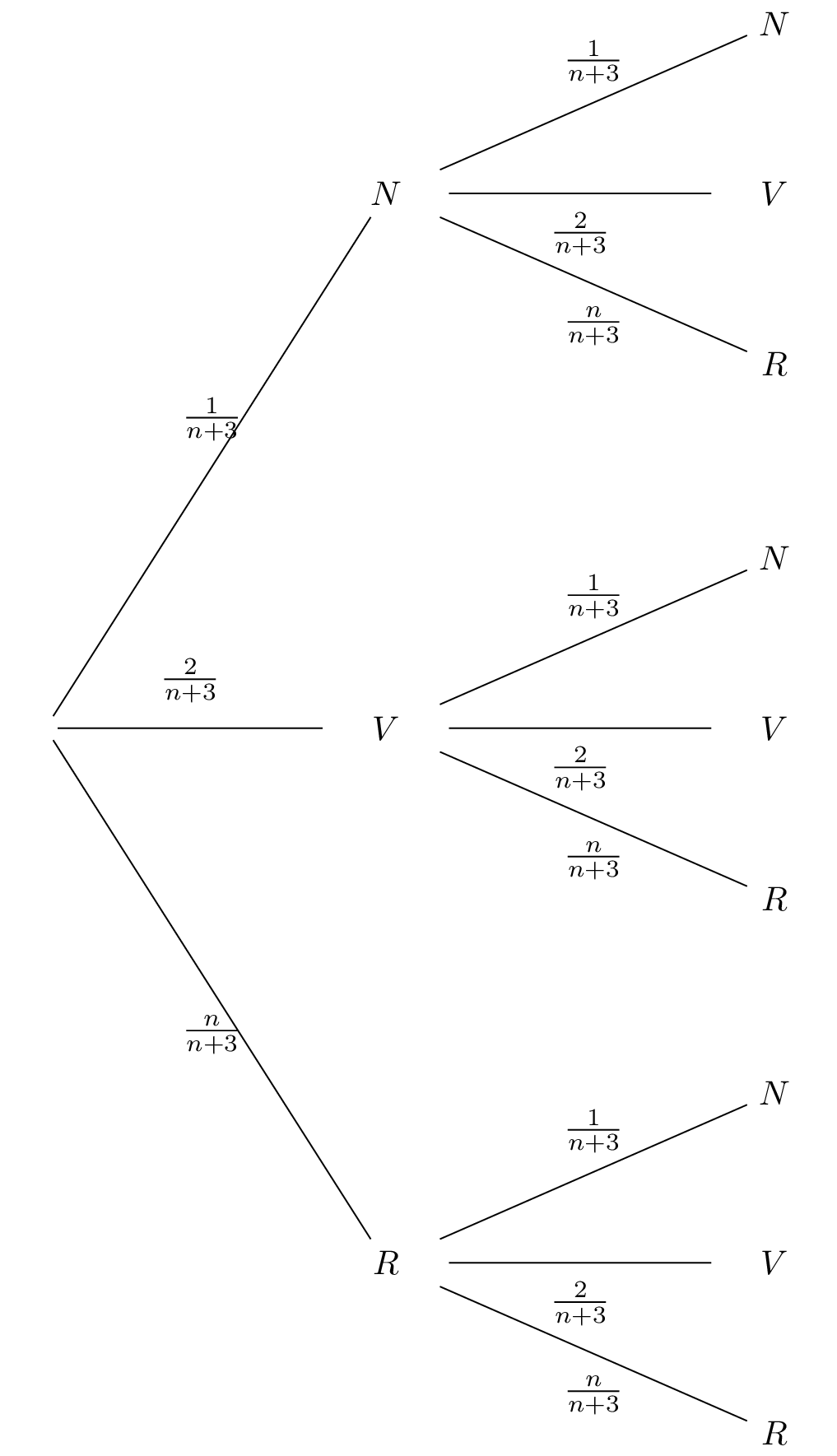

Question 2
Soit l’événement : « Les deux boules sont de la même couleur ».
Déterminer .
Correction
Pour calculer , il nous faut calculer les probabilités d'avoir rouges, noires et vertes.
Nous avons donc :
Nous avons donc :
Question 3
Soit l’événement : « Les deux boules sont de couleur différente »
Déterminer .
Correction
PREMIERE METHODE
On identifie tous les cas possibles.
DEUXIEME METHODE
Ainsi :
On identifie tous les cas possibles.
DEUXIEME METHODE
On appelle événement contraire d’un événement , l’événement noté tel que :
Les évènements et sont des événements contraires. En effet, si on prend tous les autres cas sauf ceux de l'évènement , nous aurons alors ceux de l'évènement .Ainsi :
Question 4
On considère le jeu suivant :
Le joueur perd euros si est réalisé. Le joueur gagne euros si est réalisé. On appelle la variable aléatoire égale au gain (positif ou négatif) du joueur.
Déterminer la loi de probabilité de .
Correction
Soit l’événement : « Les deux boules sont de la même couleur ».
Soit l’événement : « Les deux boules sont de couleur différente ».
D'après les questions et , la loi de probabilité de est donnée ci-dessous :
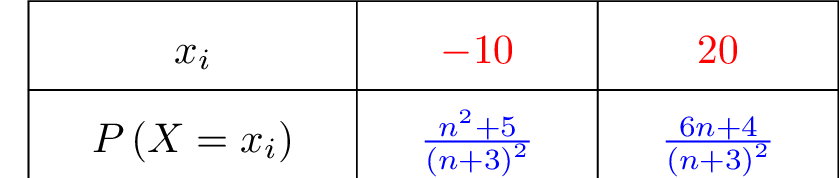
Soit l’événement : « Les deux boules sont de couleur différente ».
D'après les questions et , la loi de probabilité de est donnée ci-dessous :
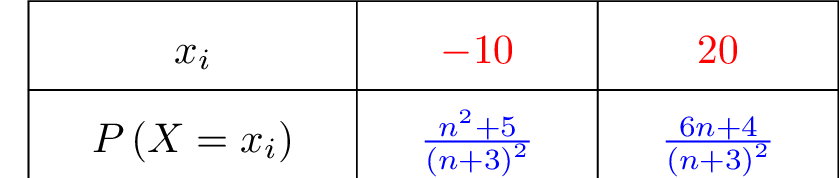
Question 5
Démontrer que .
Correction
On appelle l’espérance mathématique de la variable , la quantité notée définie par :
Ainsi :
Question 6
Pour quelles valeurs de le jeu est favorable au joueur?
Correction
- Pour que le jeu soit favorable au joueur, il faut que l'espérance soit strictement positive. Car si l'espérance est nulle, on dit que le jeu est équitable.
Pour cela, nous allons dresser un tableau de signe. Il est facile de voir que le dénominateur car .
Donc le signe de dépend du numérateur .
Il s'agit d'un trinôme du second degré.
; ; . alors la parabole est tournée vers le bas. Il en résulte donc que :
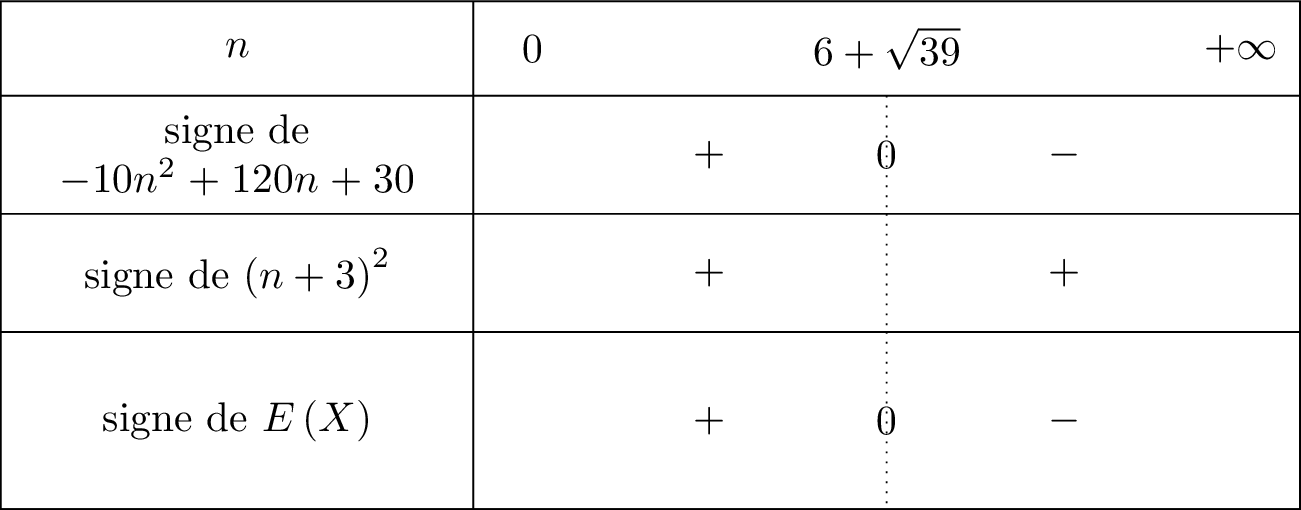
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.