Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Lecture graphique : nombre dérivé - Exercice 2
6 min
10
Question 1
A l'aide de la représentation graphique ci-dessous de la fonction :
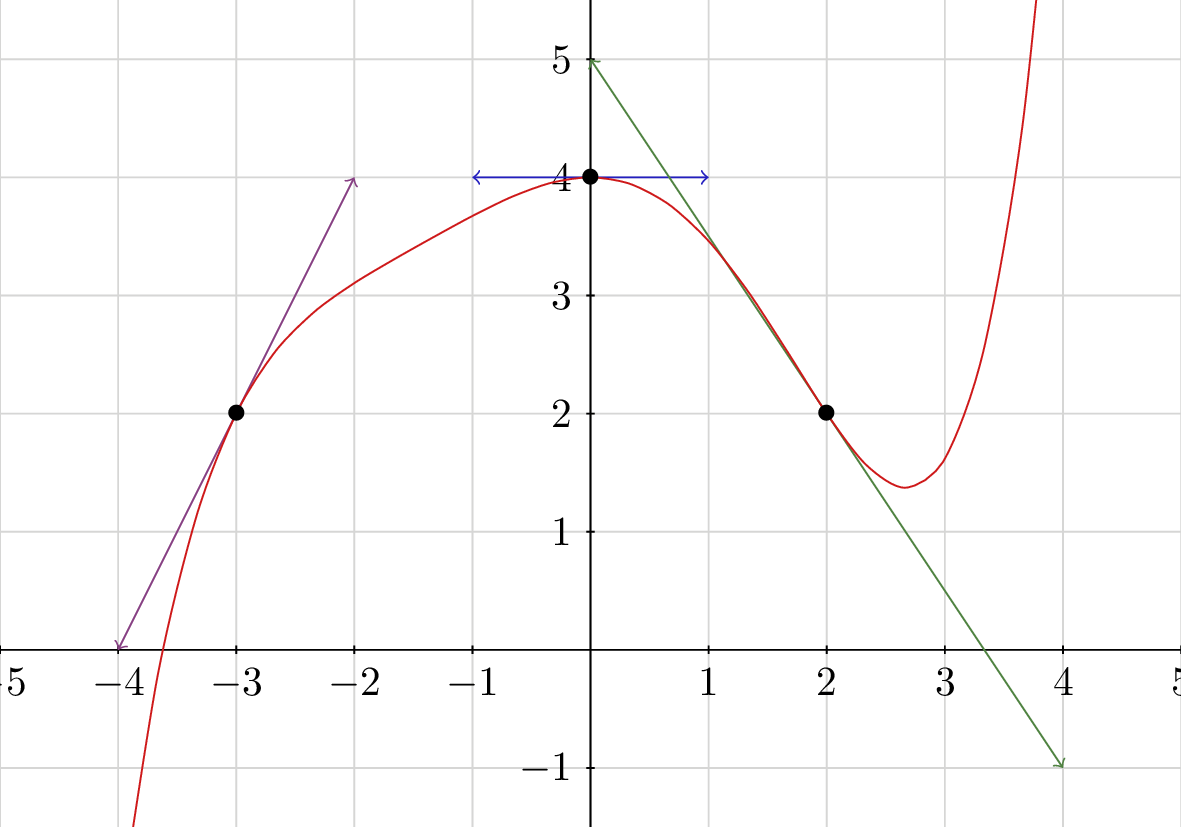 Donner les valeurs de :
Donner les valeurs de :

; et .
Correction

Question 2
Correction
correspond au coefficient directeur de la tangente à la courbe au point d'abscisse . (Ici la tangente est violette)
 Les points et appartiennent à cette tangente.
Les points et appartiennent à cette tangente.
A l'aide du point et du point on va pouvoir donner le coefficient directeur de la tangente.
Ainsi :

A l'aide du point et du point on va pouvoir donner le coefficient directeur de la tangente.
Ainsi :
Question 3
Correction
correspond au coefficient directeur de la tangente à la courbe au point d'abscisse . (Ici la tangente est bleue)
 La tangente est horizontale. Cela signifie que le coefficient directeur est nul.
La tangente est horizontale. Cela signifie que le coefficient directeur est nul.
Ainsi :

Ainsi :
Question 4
Correction
correspond au coefficient directeur de la tangente à la courbe au point d'abscisse . (Ici la tangente est violette)
 Les points et appartiennent à cette tangente.
Les points et appartiennent à cette tangente.
A l'aide du point et du point on va pouvoir donner le coefficient directeur de la tangente.
Ainsi :

A l'aide du point et du point on va pouvoir donner le coefficient directeur de la tangente.
Ainsi :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.