Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient fin janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ème partie - Exercice 2
12 min
30
C'est la finale de la Champions League. Le PSG est en finale .
Nous sommes à la ème minutes. Kylian Mbappé est lancé dans la profondeur par une passe lumineuse de Neymar. Mbappé est seul contre le gardien . Il effectue un lob est c'est le BUT !!!!!!!!
Nous sommes à la ème minutes. Kylian Mbappé est lancé dans la profondeur par une passe lumineuse de Neymar. Mbappé est seul contre le gardien . Il effectue un lob est c'est le BUT !!!!!!!!
Question 1
Ce lob est représenté, ci-dessous, dans un repère orthonormé sous la forme d'une parabole avec une de ces tangentes.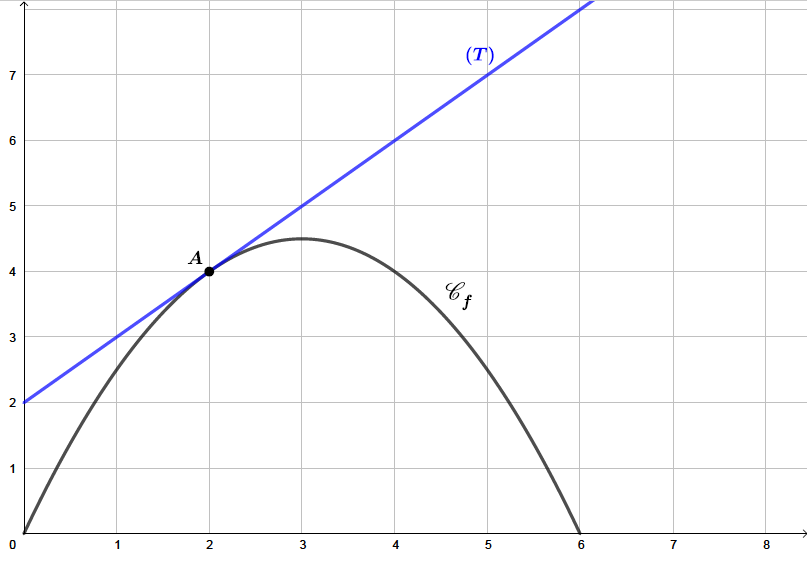

A l'aide des informations fournies par le repère, déterminer l'équation de cette parabole .
Correction
L'équation d'une parabole est de la forme où , et sont des réels.
D'après la représentation nous pouvons lire que :
Nous allons expliquer comment nous avons obtenu . La droite admet comme coefficient directeur la valeur . En effet, le coefficient directeur de la tangente au point d'abscisse correspond au nombre dérivée et de ce fait .
A partir de ces informations nous allons écrire un système d'équation :
équivaut à ce qui donne : équivaut à ce qui donne : d'où De plus, ainsi . Or : . Il vient alors que :
d'où
Nous avons donc un système deux équations à deux inconnues .
Nous allons résoudre le système à l'aide de la méthode par substitution. Pour cela, on cherche une inconnue dont le coefficient vaut . Ici, à la première ligne du système nous avons . Nous allons donc exprimer en fonction de . Il vient alors que :
. Nous allons maintenant remplacer par dans la deuxième ligne .
. Maintenant, nous connaissons la valeur de , il suffit de remplacer dans la première ligne le par . Il vient :
Le couple solution du système est alors :
Nous connaissons maintenant les valeurs de , et . Nous pouvons donc écrire que :
D'après la représentation nous pouvons lire que :
Nous allons expliquer comment nous avons obtenu . La droite admet comme coefficient directeur la valeur . En effet, le coefficient directeur de la tangente au point d'abscisse correspond au nombre dérivée et de ce fait .
A partir de ces informations nous allons écrire un système d'équation :
d'où
Nous avons donc un système deux équations à deux inconnues .
Nous allons résoudre le système à l'aide de la méthode par substitution. Pour cela, on cherche une inconnue dont le coefficient vaut . Ici, à la première ligne du système nous avons . Nous allons donc exprimer en fonction de . Il vient alors que :
. Nous allons maintenant remplacer par dans la deuxième ligne .
. Maintenant, nous connaissons la valeur de , il suffit de remplacer dans la première ligne le par . Il vient :
Le couple solution du système est alors :
Nous connaissons maintenant les valeurs de , et . Nous pouvons donc écrire que :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.